To tylko jedna z 11 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


W niniejszej notatce poruszone zostały następujące zagadnienia: asymptota pionowa lewostronna, asymptota pionowa prawostronna, asymptota pionowa obustronna, krzywa. Ponadto w dokumencie pojawiają się takie zagadnienia jak: asymptota ukośna prawostronna, asymptota ukośna lewostronna, asymptota ukośna obustronna.Notatka zawiera informacje na temat: co to jest asymptota pozioma lewostronna, asymptota pozioma prawostronna oraz co to jest asymptota pozioma obustronna.
Asymptoty
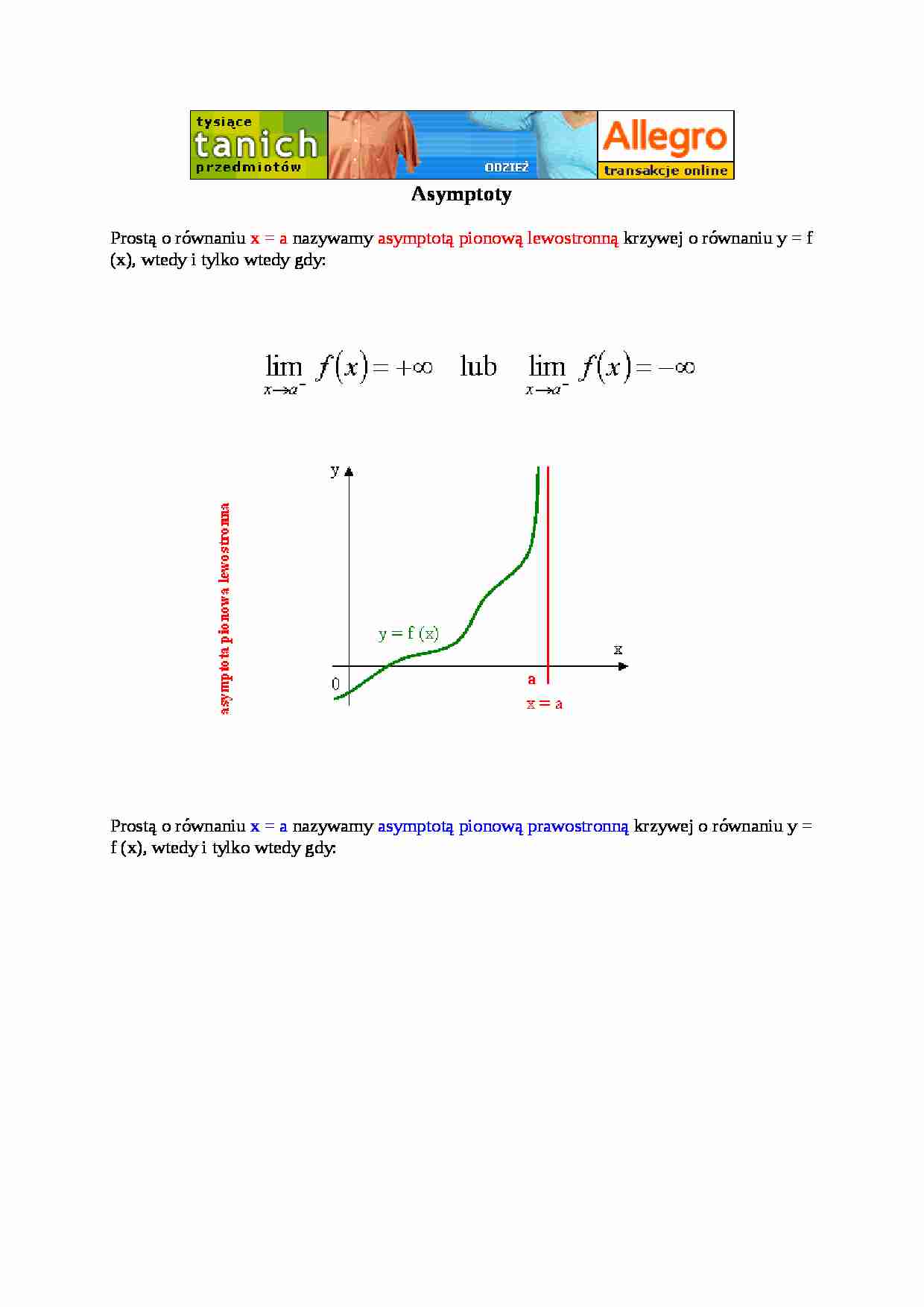
Prostą o równaniu x = a nazywamy asymptotą pionową lewostronną krzywej o równaniu y = f (x), wtedy i tylko wtedy gdy:
Prostą o równaniu x = a nazywamy asymptotą pionową prawostronną krzywej o równaniu y = f (x), wtedy i tylko wtedy gdy:
Prostą x = a nazywamy asymptotą pionową obustronną krzywej y = f (x), wtedy i tylko wtedy gdy jest jednocze�nie asymptotą pionową prawostronną i asymptotą pionową lewostronną danej krzywej. Prostą o równaniu y = mx + k, gdzie m ≠ 0 nazywamy asymptotą uko�ną prawostronną krzywej o równaniu y = f(x), wtedy i tylko wtedy gdy :
Prostą o równaniu y = mx + k, gdzie m ≠ 0 nazywamy asymptotą uko�ną lewostronną krzywej o równaniu y = f(x), wtedy i tylko wtedy gdy :
Prostą o równaniu y = mx + k, gdzie m ≠ 0 nazywamy asymptotą uko�ną obustronną krzywej y = f (x), wtedy i tylko wtedy gdy jest jednocze�nie asymptotą uko�ną prawostronną i asymptotą uko�ną lewostronną danej krzywej. Prostą o równaniu y = b nazywamy asymptotą poziomą lewostronną krzywej o równaniu y = f (x), wtedy i tylko wtedy gdy:
Prostą o równaniu y = b nazywamy asymptotą poziomą prawostronną krzywej o równaniu y = f (x), wtedy i tylko wtedy gdy:
Prostą o równaniu y = b, nazywamy asymptotą poziomą obustronną krzywej y = f (x), wtedy i tylko wtedy gdy jest jednocze�nie asymptotą poziomą prawostronną i asymptotą poziomą lewostronną danej krzywej.
... zobacz całą notatkę






Komentarze użytkowników (0)