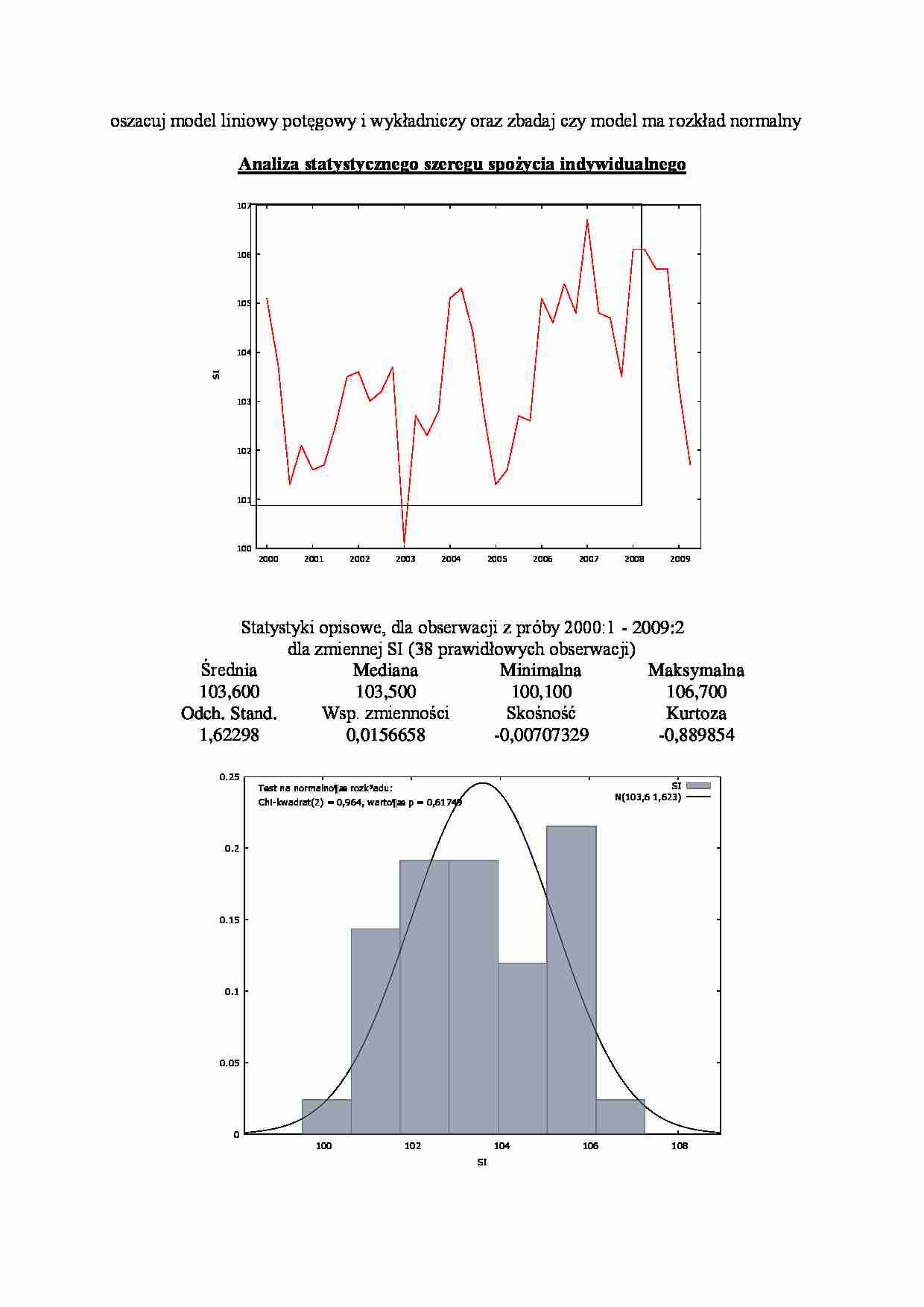
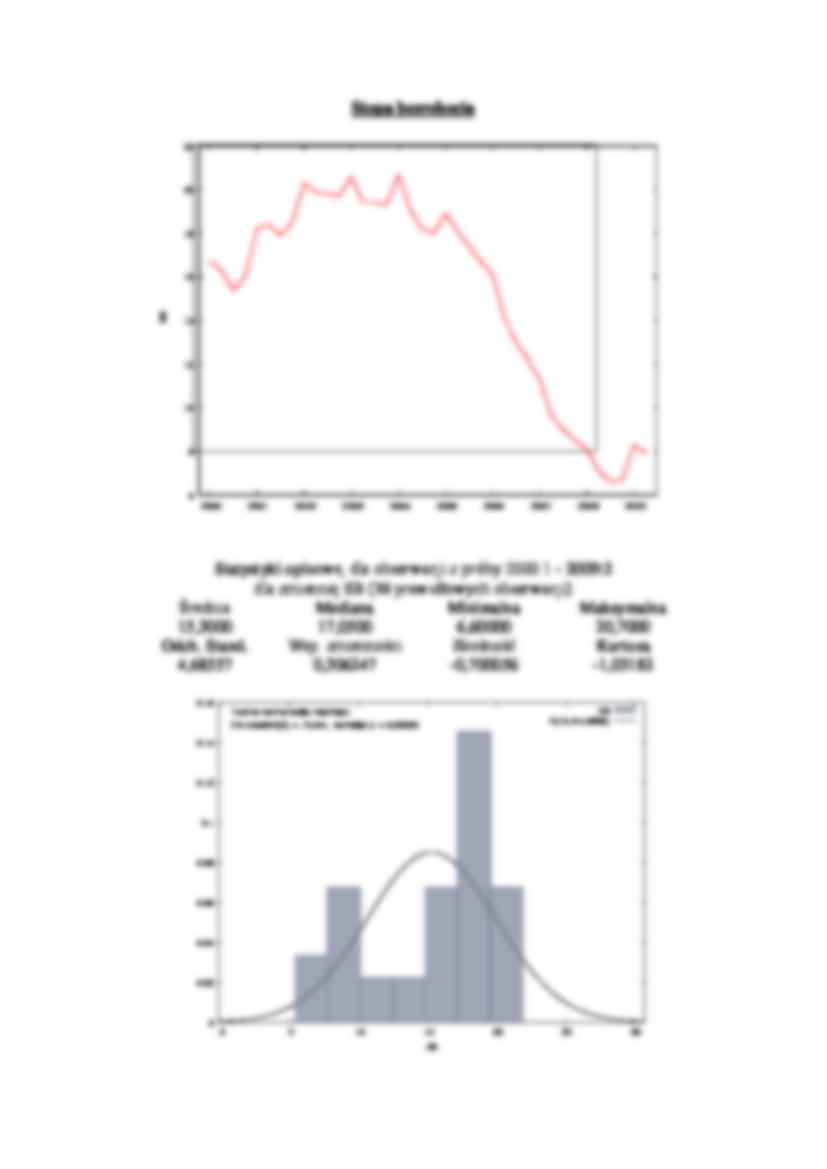
oszacuj model liniowy potęgowy i wykładniczy oraz zbadaj czy model ma rozkład normalny Analiza statystycznego szeregu spożycia indywidualnego 100 101 102 103 104 105 106 107 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 SI Statystyki opisowe, dla obserwacji z próby 2000:1 - 2009:2 dla zmiennej SI (38 prawidłowych obserwacji) Średnia Mediana Minimalna Maksymalna 103,600 103,500 100,100 106,700 Odch. Stand. Wsp. zmienności Skośność Kurtoza 1,62298 0,0156658 -0,00707329 -0,889854 0 0.05 0.1 0.15 0.2 0.25 100 102 104 106 108 Gêsto¶æ SI SI N(103,6 1,623) Test na normalno¶æ rozk³adu: Chi-kwadrat(2) = 0,964, warto¶æ p = 0,61749 Analiza statystyczna wynagrodzenia przeciętnego 100 101 102 103 104 105 106 107 108 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 PW Statystyki opisowe, dla obserwacji z próby 2000:1 - 2009:2 dla zmiennej PW (38 prawidłowych obserwacji) Średnia Mediana Minimalna Maksymalna 102,979 102,500 100,300 107,800 Odch. Stand. Wsp. zmienności Skośność Kurtoza 1,98741 0,0192992 0,648278 -0,415076 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 0.2 0.22 98 100 102 104 106 108 Gêsto¶æ PW PW N(102,98 1,9874) Test na normalno¶æ rozk³adu: Chi-kwadrat(2) = 5,639, warto¶æ p = 0,05963 Stopa bezrobocia 6 8 10 12 14 16 18 20 22 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 SB Statystyki opisowe, dla obserwacji z próby 2000:1 - 2009:2 dla zmiennej SB (38 prawidłowych obserwacji) Średnia Mediana Minimalna Maksymalna 15,3000 17,0500 6,60000 20,7000 Odch. Stand. Wsp. zmienności Skośność Kurtoza 4,68557 0,306247 -0,700056 -1,03182 0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0 5 10 15 20 25 30 Gêsto¶æ SB SB N(15,3 4,6856) Test na normalno¶æ rozk³adu: Chi-kwadrat(2) = 19,641, warto¶æ p = 0,00005 Współczynniki korelacji liniowej dla obserwacji z próby 2000:1-2009:2 Wartość krytyczna (przy dwustronnym 5% obszarze krytycznym) = 0,3202 dla n = 38 SI PW SB 1,0000 0,6291 -0,5103 SI 1,0000 -0,6698 PW 1,0000 SB Model liniowy
(…)
…. Schwarza 134,4852 Kryt. Hannana-Quinna 131,3203
Autokorel.reszt - rho1 0,399443 Stat. Durbina-Watsona 1,181527
H 0 : t ~ N
H A : t ~ N
c12 (c2 3) 2
JB T { }
6 24
1) JB (2) prob
2
2) JB (2) prob
2
C1 współczynnik skośności reszt
C2 wspułczynnik spłaszczenia reszt
Nie ma podstaw do odrzucenia h0 to oznacza ze składniki losowy ma rozkład normalny
Odrzucamy h0 na rzecz HA a wiec…
…-kwadrat(2) = 19,641, warto¶æ p = 0,00005
0.14
0.12
Gêsto¶æ
0.1
0.08
0.06
0.04
0.02
0
0
5
10
15
SB
20
25
30
Współczynniki korelacji liniowej dla obserwacji z próby 2000:1-2009:2
Wartość krytyczna (przy dwustronnym 5% obszarze krytycznym) = 0,3202 dla n = 38
SI
1,0000
PW
0,6291
1,0000
SB
-0,5103
-0,6698
1,0000
SI
PW
SB
Model liniowy
SIt 0 1PWt 2 SBt
Model 1: Estymacja KMNK, wykorzystane obserwacje 2000:1-2009:2 (N = 38)
Zmienna zależna: SI
Współczynnik Błąd stand.
Const(wyraz wolny)
60,6345
15,3397
PW
0,425526
0,14277
SB
-0,0558663 0,0605569
Średn.aryt.zm.zależnej
Suma kwadratów reszt
Wsp. determ. R-kwadrat
F(2, 35)
Logarytm wiarygodności
Kryt. bayes. Schwarza
Autokorel.reszt - rho1
103,6000
57,49021
0,410115
12,16679
-61,78621
134,4852
0,399443
t-Studenta
3,9528
2,9805
-0,9225
wartość p
0,00036
0,00521
0,36256
Odch.stand.zm.zależnej
Błąd standardowy reszt
Skorygowany R-kwadrat
Wartość p dla testu F
Kryt. inform. Akaike'a
Kryt. Hannana-Quinna
Stat. Durbina-Watsona
***
***
1,622977
1,281631
0,376407
0,000097
129,5724
131,3203
1,181527
H 0 : t ~ N
H A : t ~ N
c12 (c2 3) 2
}
6
24
2
1) JB (2) prob
JB T {
2
2) JB (2) prob
C1 współczynnik skośności reszt
C2…
... zobacz całą notatkę




Komentarze użytkowników (0)