To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
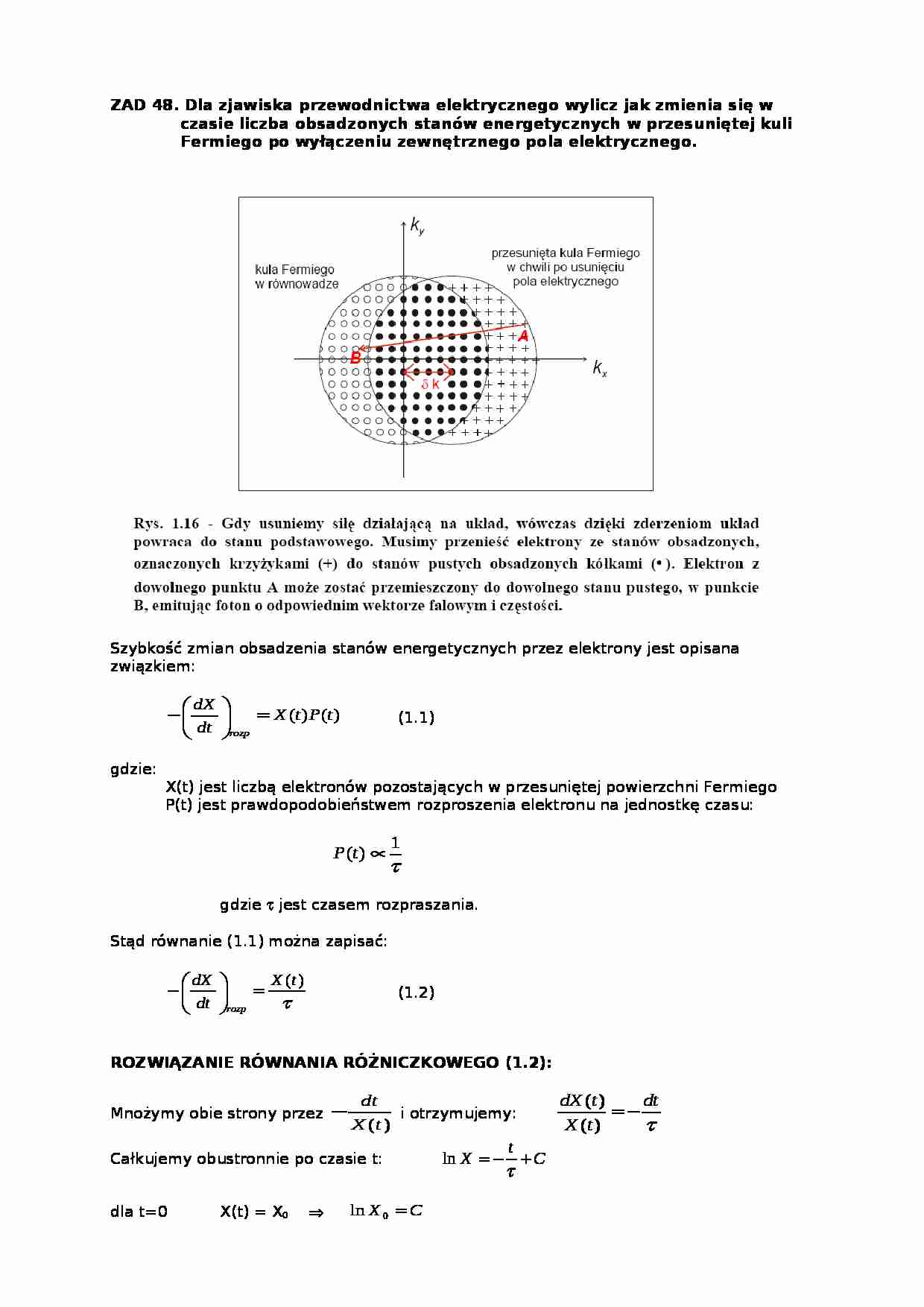


ZAD 48. Dla zjawiska przewodnictwa elektrycznego wylicz jak zmienia się w czasie liczba obsadzonych stanów energetycznych w przesuniętej kuli Fermiego po wyłączeniu zewnętrznego pola elektrycznego. Szybkość zmian obsadzenia stanów energetycznych przez elektrony jest opisana związkiem: ) ( ) ( t P t X dt dX rozp (1.1) gdzie: X(t) jest liczbą elektronów pozostających w przesuniętej powierzchni Fermiego P(t) jest prawdopodobieństwem rozproszenia elektronu na jednostkę czasu: 1 ) ( t P gdzie jest czasem rozpraszania. Stąd równanie (1.1) można zapisać: ) ( t X dt dX rozp (1.2) ROZWIĄZANIE RÓWNANIA RÓŻNICZKOWEGO (1.2): Mnożymy obie strony przez ) ( t X dt i otrzymujemy: dt t X t dX ) ( ) ( Całkujemy obustronnie po czasie t: C t X ln dla t=0 X(t) = X0 C X 0 ln Dalsze przekształcenia: 0 ln ln X t X t X X 0 ln ln t X X 0 ln t e X X 0 t e X t X 0 ) ( Wyrażenie końcowe wskazuje na eksponencjalny spadek zapełnienia stanów energetycznych przez elektrony w przesuniętej powierzchni Fermiego. Po czasie t z X0 elektronów zostało w przesuniętej kuli X(t) elektronów.
... zobacz całą notatkę






Komentarze użytkowników (0)