Zastosowania geometryczne całki oznaczonej

Nasza ocena:

3
Pobrań: 154
Wyświetleń: 756
Komentarze: 0
Notatek.pl

Pobierz ten dokument za darmo

Pobierz notatkę
Podgląd dokumentu
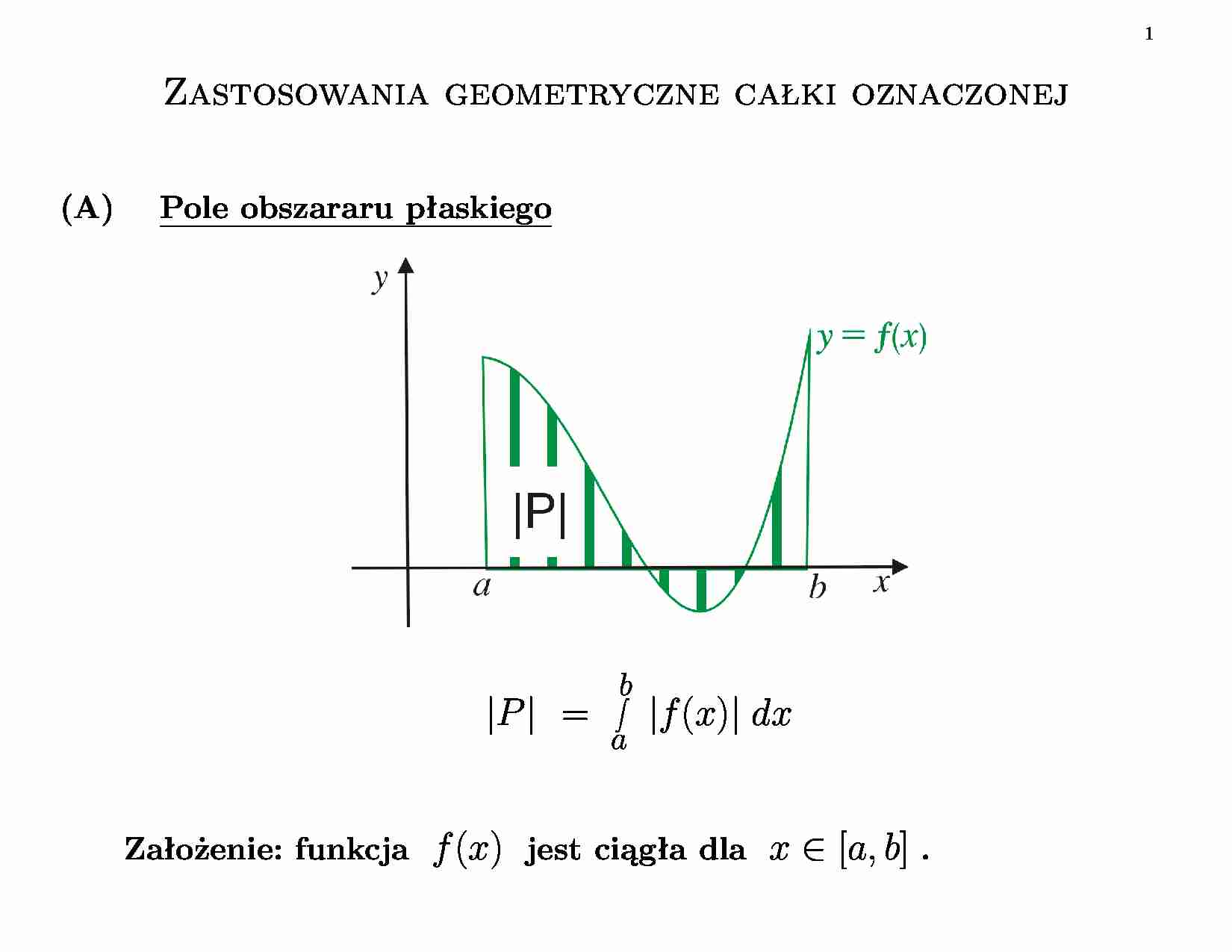
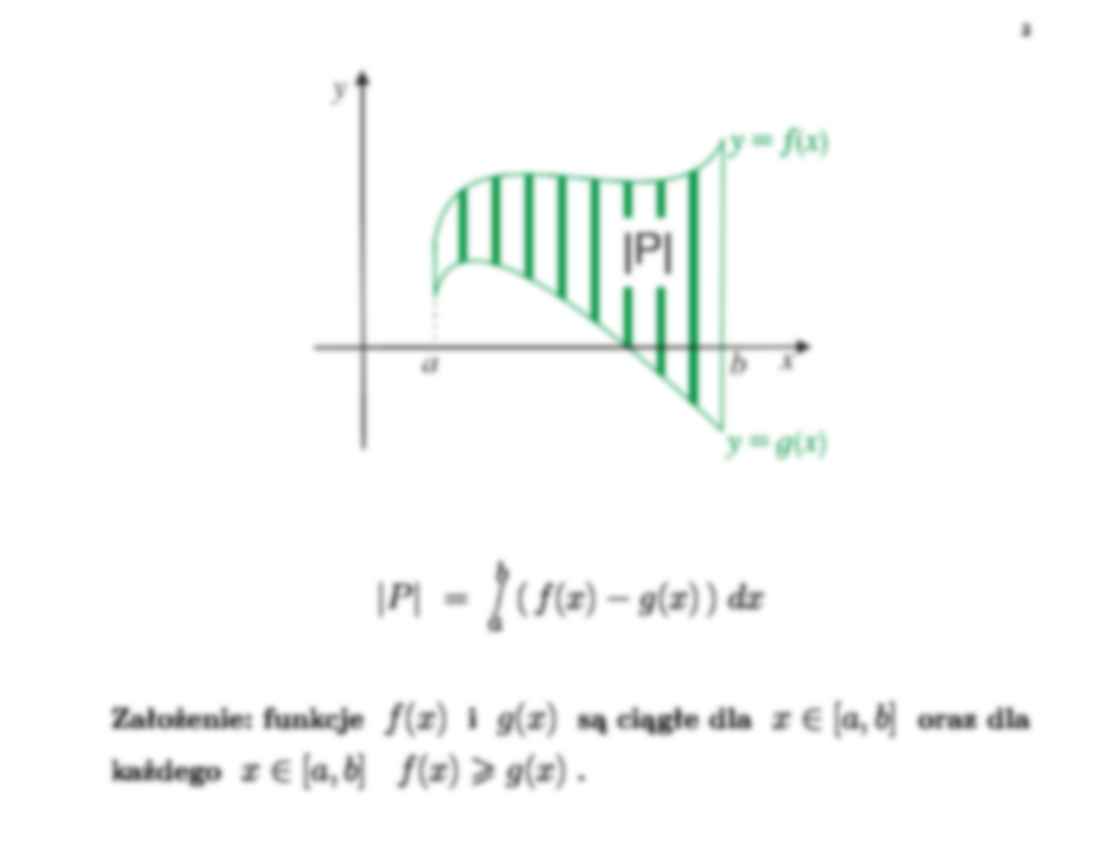
Zastosowania geometryczne całki oznaczonej - strona 1 Zastosowania geometryczne całki oznaczonej - strona 2 Zastosowania geometryczne całki oznaczonej - strona 3

Fragment notatki:


1 Zastosowania geometryczne całki oznaczonej (A) Pole obszararu płaskiego |P |  = b a |f  ( x ) | dx Założenie: funkcja f  ( x )  jest ciągła dla  x ∈  [ a, b ]  . 2 |P |  = d c |f  ( y ) | dy Założenie: funkcja f  ( y )  jest ciągła dla  y ∈  [ c, d ]  . 3 |P |  = b a (  f  ( x )  − g ( x ) )  dx Założenie: funkcje f  ( x )  i  g ( x )  są ciągłe dla  x ∈  [ a, b ]  oraz dla każdego x ∈  [ a, b ]  f  ( x ) g ( x )  . 4 |P |  = d c (  f  ( y )  − g ( y ) )  dy Założenie: funkcje f  ( y )  i  g ( y )  są ciągłe dla  y ∈  [ c, d ]  oraz dla każdego y ∈  [ c, d ]  f  ( y ) g ( y )  . 5 Przykład Oblicz pola obszarów ograniczonych wykresami funkcji: a) y  = arctg  x, y  = 1  − ex, x  = 1 b) y  = ln  x, y  =  − 1 , y  = 1 , x  = 0 (B) Krzywa płaska zadana parametrycznie Definicja Zbiór punktów płaszczyzny ( x, y )  ∈  R 2  taki, że                      x  =  x ( t ) t ∈  [ t 1 , t 2] y  =  y ( t ) gdzie x ( t ) i y ( t ) są funkcjami ciągłymi dla t ∈  [ t 1 , t 2] nazywamy  krzywą płaską daną parametrycznie . Punkt ( x ( t 1) , y ( t 1)) nazywamy  początkiem krzywej , punkt ( x ( t 2) , y ( t 2))  -  końcem . 6 Przykład •  Prosta przechodząca przez punkt P  ( x 0 , y 0)  i równoległa do wektora a  = [ a 1 , a 2]  ma parametryzację:                      x ( t ) =  x 0 +  a 1  t t ∈  R y ( t ) =  y 0 +  a 2  t Jeżeli y ∈  [ t 1 , t 2]  , to wzór powyższy przedstawia parametryzację odcinka o początku w punkcie ( x ( t 1) , y ( t 1))  i końcu w punkcie ( x ( t 2) , y ( t 2))  . •  Odcinek o początku w punkcie A ( xA, yA )  i końcu w punkcie B ( xB, yB )  ma parametryzację:                      x ( t ) =  xA  + ( xB − xA )  t t ∈  [0 ,  1] y ( t ) =  yA  + ( yB − yA )  t 7 •  Okrąg o środku w punkcie P  ( x 0 , y 0)  i promieniu  R   0  ma parametryzację:                      x ( t ) =  x 0 +  R  cos  t t ∈  [0 ,  2 π ] y ( t ) =  y 0 +  R  sin  t •  Elipsa o równaniu x 2 a 2 + y 2 b 2 = 1 ma parametryzację:     

(…)

… z
z dz
−2




3 sin z



 y(t)
=



z dz
t
x(t) =
16
(H)
Długość łuku krzywej we współrzędnych biegunowych
|L| =
β
α
(r(ϕ))2 + (r (ϕ))2 dϕ
Założenie: funkcje r(ϕ) i r (ϕ) są ciągłe dla ϕ ∈ [α, β] .
Przykład
Oblicz
długość
łuku
krzywej
r(ϕ) = a(1 + cos ϕ) , gdzie a > 0 i ϕ ∈ [0, 2π] .
o
równaniu
17
(I)
Objętość bryły obrotowej powstałej przez obrót wykresu funkcji
dookoła osi 0X
|V | = π
b…
… we współrzędnych biegunowych:
a) x2 + y 2 = R2
b)
( x2 + y 2 )2 = a2 ( x2 − y 2 ),
a>0
12
(E)
Pole obszaru płaskiego pod krzywą zadaną we współrzędnych
biegunowych
1 β 2
|P | =
r (ϕ) dϕ
2 α
Założenie: funkcja r(ϕ) jest ciągła i nieujemna dla ϕ ∈ [α, β] .
Przykład Oblicz pole obszaru ograniczonego krzywą z punktu b)
z poprzedniego przykładu.
13
(F)
Długość łuku wykresu funkcji
|L| =
b
a
1 + (f (x))2 dx
Założenie…
... zobacz całą notatkę



Komentarze użytkowników (0)

Zaloguj się, aby dodać komentarz