Wybrane zadania z kartkówek w latach 2004 — 2007
1.
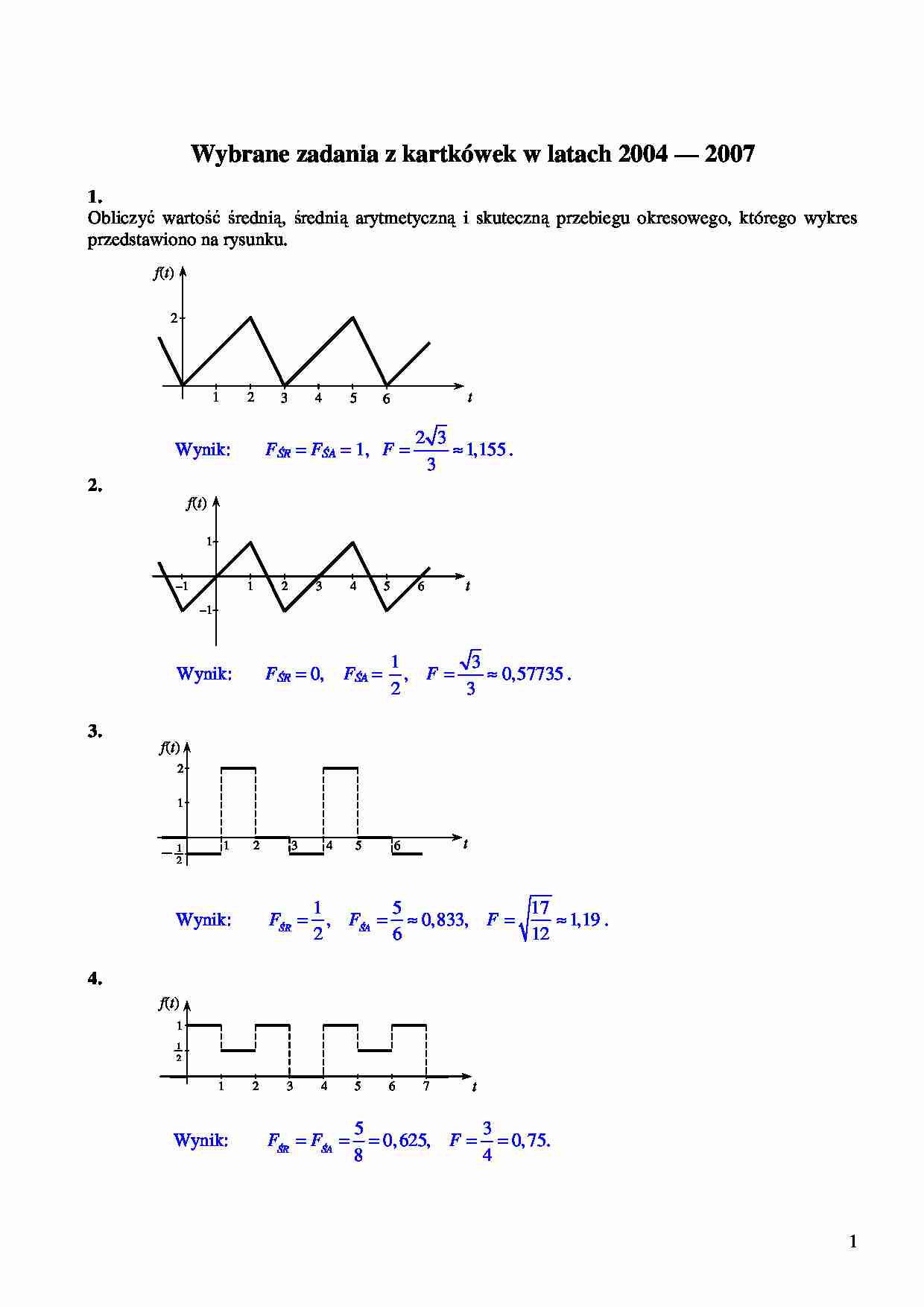
Obliczyć wartość średnią, średnią arytmetyczną i skuteczną przebiegu okresowego, którego wykres
przedstawiono na rysunku.
f(t)
2
1
2
3
4
5
t
6
FŚR = FŚA = 1, F =
Wynik:
2 3
≈ 1,155 .
3
2.
f(t)
1
–1
1
2
3
4
5
6
t
–1
Wynik:
FŚR = 0,
FŚA =
1
3
, F=
≈ 0,57735 .
2
3
3.
f(t)
2
1
−1
2
1
2
3
4
5
t
6
1
5
17
FŚR = , FŚA = ≈ 0,833, F =
≈ 1,19 .
2
6
12
Wynik:
4.
f(t)
1
1
2
1
Wynik:
2
3
4
FŚR = FŚA =
5
6
7
t
5
3
= 0, 625, F = = 0, 75.
8
4
1
5.
f(t)
1
1
3
2
4
5
6
7
t
–1
1
3
FŚR = 0, FŚA = , F =
≈ 0, 5774 .
2
3
Wynik:
6.
f(t)
1
1
2
3
t
1
3
FŚR = FŚA = , F =
≈ 0,5774 .
2
3
Wynik:
7.
f(t)
1
1
Wynik:
2
3
FŚR = FŚA =
t
4
1
1
≈ 0,3183, F = .
π
2
8.
f(t)
1
1
Wynik:
9.
2
3
4
5
6
t
1
1
FŚR = FŚA = ≈ 0,3183, F = .
π
2
f(t)
1
7π
2
3π
2
π
2π
3π
4π
t
–1
Wynik:
FŚR =
1
3
6
≈ 0,1592, FŚA =
≈ 0, 4775, F =
≈ 0, 6124 .
2π
2π
4
2
10.
W obwodzie przedstawionym na rysunku klucz K był rozwarty przez nieskończenie długi czas.
W chwili t = 0 klucz ten został zwarty. Wyznaczyć napięcie u(t), t ≥ 0 .
K
R1
t=0
Dane:
E0 = 12 V = const,
R2
u(t)
L
E0
R1 = 1 ,
Wynik:
R2 = 3 ,
L=
1
H.
2
u ( t ) = 9e −2 t V.
11.
W obwodzie przedstawionym na rysunku klucz K był zwarty przez nieskończenie długi czas.
W chwili t = 0 klucz ten został rozwarty. Wyznaczyć prąd i(t), t ≥ 0 .
R1
K
i(t)
t=0
E0
Dane:
E0 = 8 V = const,
C
R1 = 3 ,
R2
Wynik:
i ( t ) = 2e
R2 = 1 ,
C = 2 F.
1
− t
6
A.
12.
W obwodzie przedstawionym na rysunku klucz K był zwarty przez nieskończenie długi czas.
W chwili t = 0 klucz ten został rozwarty. Wyznaczyć napięcie u(t), t ≥ 0 .
t=0
K
R1
Iz0
R2
C
u(t)
Dane:
I z0 = 3 A = const,
R1 = 1 ,
Wynik:
u ( t ) = 2e
1
− t
2
R2 = 2
C = 1 F.
,
V.
13.
W obwodzie przedstawionym na rysunku klucz K był zwarty przez nieskończenie długi czas.
W chwili t = 0 klucz ten został rozwarty. Wyznaczyć napięcie u(t), t ≥ 0 .
K
Iz0
R1
Wynik:
Dane:
I z0 = 2 A = const,
R2
L
t=0
u(t)
R1 =
3
2
,
R2 =
1
2
,
L = 1 H.
u ( t ) = 3e −2 t V.
3
14.
W obwodzie przedstawionym na rysunku klucz K był zwarty przez nieskończenie długi czas.
W chwili t = 0 klucz ten został rozwarty. Wyznaczyć prąd i(t), t ≥ 0 .
K
i(t)
t=0
Iz0
R2
Dane:
I z0 = 4 A = const,
C
R1
R1 = 1 ,
1
6
− t
i ( t ) = 3e
Wynik:
R2 = 3 ,
C = 2 F.
A.
15.
W obwodzie przedstawionym na rysunku klucz K był rozwarty przez nieskończenie długi czas.
W chwili t = 0 klucz ten został zwarty. Wyznaczyć prąd i(t), t ≥ 0 .
R1
i(t)
t=0
K
E0
Dane:
E0 = 12 V = const,
C
R2
R1 = 5
,
R2 = 1 ,
C=
1
5
F.
i ( t ) = −12e −6t A.
Wynik:
16.
W obwodzie przedstawionym na rysunku klucz K był zwarty przez nieskończenie długi czas.
W chwili t = 0 klucz ten został rozwarty. Wyznaczyć napięcie u(t), t ≥ 0 .
t=0
K
Dane:
I z0 = 3 A = const,
R2
Iz0
L
R1
Wynik:
u(t)
R1 = 2
,
R2 = 1 ,
L=
1
2
H.
u ( t ) = −3e −6 t V.
17.
W obwodzie przedstawionym na
... zobacz całą notatkę





Komentarze użytkowników (0)