Wzory pochodne całki

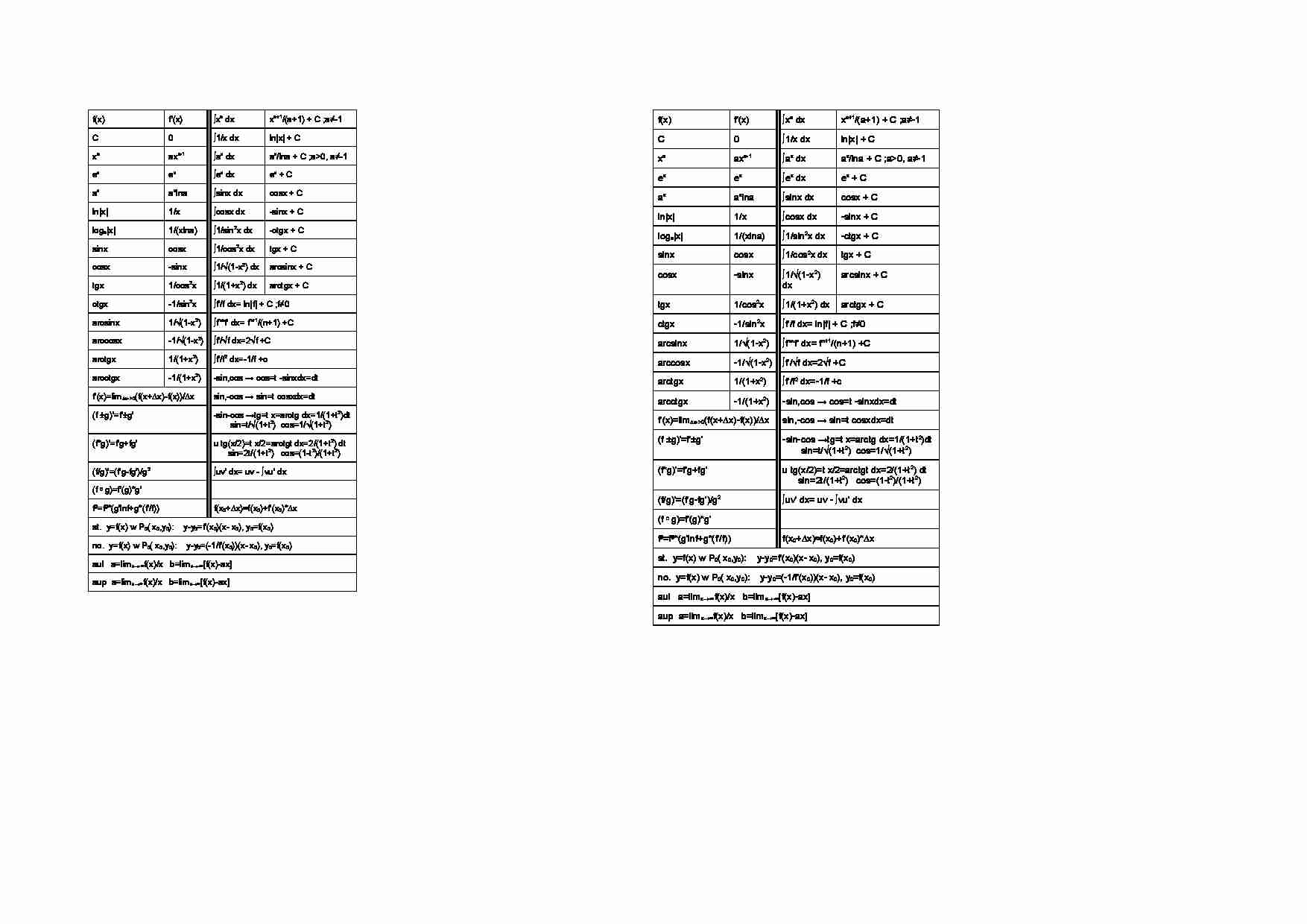
f(x) f'(x) ∫xa dx xa+1/(a+1) + C ;a≠-1 C 0 ∫1/x dx ln|x| + C xa axa-1 ∫ax dx ax/lna + C ;a0, a≠-1 ex ex ∫ex dx ex + C ax axlna ∫sinx dx cosx + C ln|x| 1/x ∫cosx dx -sinx + C loga|x| 1/(xlna) ∫1/sin2x dx -ctgx + C sinx cosx ∫1/cos2x dx tgx + C cosx -sinx ∫1/√(1-x2) dx arcsinx + C tgx 1/cos2x ∫1/(1+x2) dx arctgx + C ctgx -1/sin2x ∫f'/f dx= ln|f| + C ;f≠0 arcsinx 1/√(1-x2) ∫fn*f' dx= fn+1/(n+1) +C arccosx -1/√(1-x2) ∫f'/√f dx=2√f +C arctgx 1/(1+x2) ∫f'/f2 dx=-1/f +c arcctgx -1/(1+x2) -sin,cos → cos=t -sinxdx=dt f'(x)=lim∆x-0(f(x+∆x)-f(x))/∆x sin,-cos → sin=t cosxdx=dt (f ±g)'=f'±g' -sin-cos →tg=t x=arctg dx=1/(1+t2)dt        sin=t/√(1+t2)  cos=1/√(1+t2) (f*g)'=f'g+fg' u tg(x/2)=t x/2=arctgt dx=2/(1+t2) dt       sin=2t/(1+t2)   cos=(1-t2)/(1+t2) (f/g)'=(f'g-fg')/g2 ∫uv' dx= uv - ∫vu' dx (f  *  g)=f'(g)*g' fg=fg*(g'lnf+g*(f'/f)) f(x0+∆x)≈f(x0)+f'(x0)*∆x st.  y=f(x) w P0( x0,y0):    y-y0=f'(x0)(x- x0), y0=f(x0) no.  y=f(x) w P0( x0,y0):    y-y0=(-1/f'(x0))(x- x0), y0=f(x0) aul   a=limx→-∞f(x)/x   b=limx→-∞[f(x)-ax] aup  a=limx→∞f(x)/x   b=limx→∞[f(x)-ax] f(x) f'(x) ∫xa dx xa+1/(a+1) + C ;a≠-1 C 0 ∫1/x dx ln|x| + C xa axa-1 ∫ax dx ax/lna + C ;a0, a≠-1 ex ex ∫ex dx ex + C ax axlna ∫sinx dx cosx + C ln|x| 1/x ∫cosx dx -sinx + C loga|x| 1/(xlna) ∫1/sin2x dx -ctgx + C sinx cosx ∫1/cos2x dx tgx + C cosx -sinx ∫1/√(1-x2)  dx arcsinx + C tgx 1/cos2x ∫1/(1+x2) dx arctgx + C ctgx -1/sin2x ∫f'/f dx= ln|f| + C ;f≠0 arcsinx 1/√(1-x2) ∫fn*f' dx= fn+1/(n+1) +C arccosx -1/√(1-x2) ∫f'/√f dx=2√f +C arctgx 1/(1+x2) ∫f'/f2 dx=-1/f +c arcctgx -1/(1+x2) -sin,cos → cos=t -sinxdx=dt f'(x)=lim∆x-0(f(x+∆x)-f(x))/∆x sin,-cos → sin=t cosxdx=dt (f ±g)'=f'±g' -sin-cos →tg=t x=arctg dx=1/(1+t2)dt        sin=t/√(1+t2)  cos=1/√(1+t2) (f*g)'=f'g+fg' u tg(x/2)=t x/2=arctgt dx=2/(1+t2) dt       sin=2t/(1+t2)   cos=(1-t2)/(1+t2) (f/g)'=(f'g-fg')/g2 ∫uv' dx= uv - ∫vu' dx (f  *  g)=f'(g)*g' fg=fg*(g'lnf+g*(f'/f)) f(x0+∆x)≈f(x0)+f'(x0)*∆x st.  y=f(x) w P0( x0,y0):    y-y0=f'(x0)(x- x0), y0=f(x0) no.  y=f(x) w P0( x0,y0):    y-y0=(-1/f'(x0))(x- x0), y0=f(x0) aul   a=limx→-∞f(x)/x   b=limx→-∞[f(x)-ax] aup  a=limx→∞f(x)/x   b=limx→∞[f(x)-ax] ... zobacz całą notatkę