To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
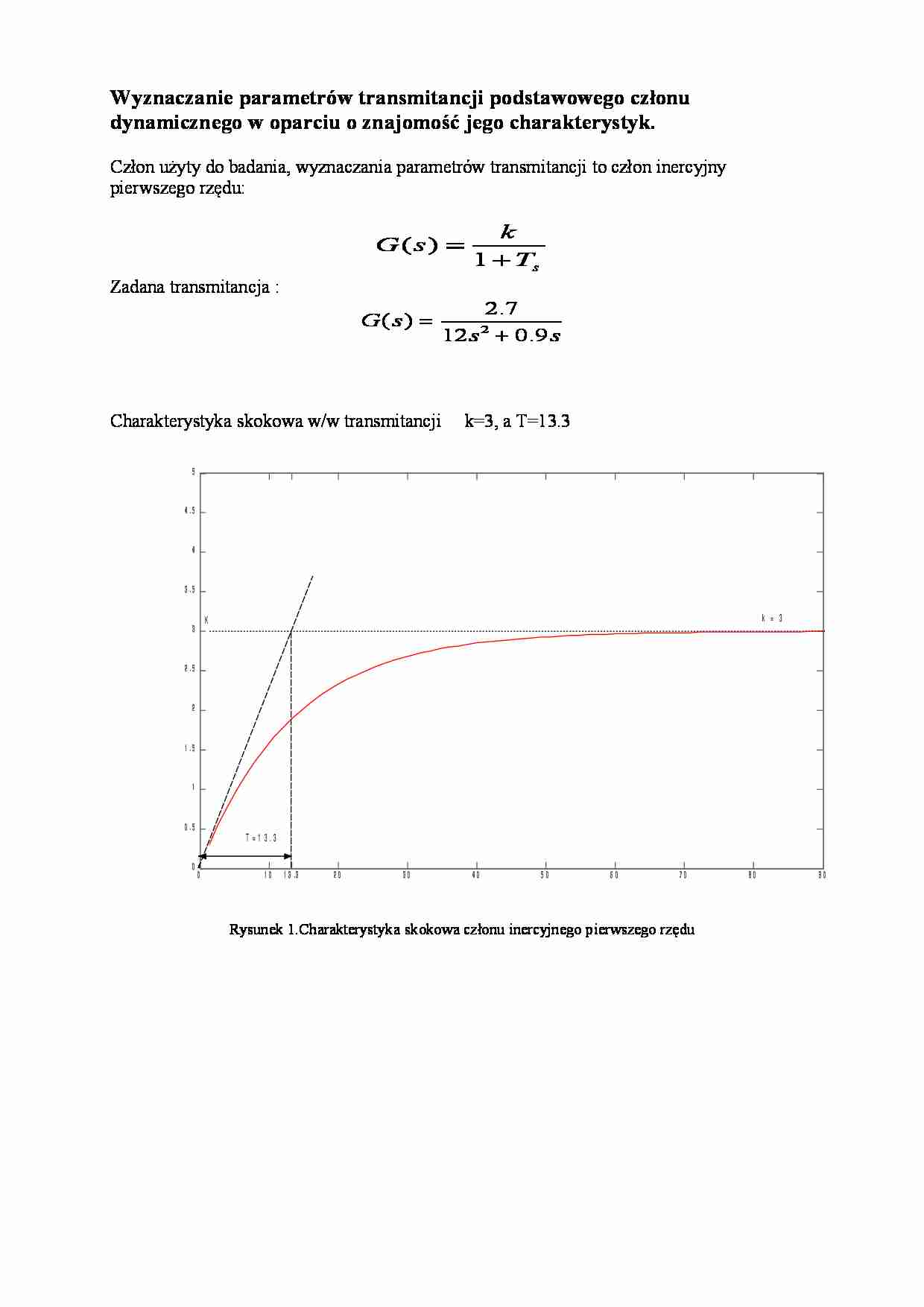


Wyznaczanie parametrów transmitancji podstawowego członu dynamicznego w oparciu o znajomość jego charakterystyk. Człon użyty do badania, wyznaczania parametrów transmitancji to człon inercyjny pierwszego rzędu: s T k s G + = 1 ) ( Zadana transmitancja : s s s G 9 . 0 12 7 . 2 ) ( 2 + = Charakterystyka skokowa w/w transmitancji k=3, a T=13.3 0 1 0 1 3 .3 2 0 3 0 4 0 5 0 6 0 7 0 8 0 9 0 0 0 . 5 1 1 . 5 2 2 . 5 3 3 . 5 4 4 . 5 5 T = 1 3 . 3 K k = 3 Rysunek 1.Charakterystyka skokowa członu inercyjnego pierwszego rzędu Logarytmiczna charakterystyka modułu i fazy badanego członu C h a r a k t e r y s t y k a s k o k o w a C z e s t o t l i w o s c ( r a d / s e c ) - 6 0 - 4 0 - 2 0 0 2 0 3 6 .8 4 5 6 0 M od ul (d B ) 0 . 0 0 1 0 . 0 1 0 . 0 7 3 0 . 1 1 1 0 - 1 8 0 - 1 3 5 - 9 0 Fa za (d eg ) g L m = 3 8 . 6 w = 1 / w 0 ( - 1 3 5 ) = 0 . 0 7 3 T = 1 / w = 1 3 .6 9 w 0 = 0 . 0 7 8 T = 1 / w 0 = 1 2 . 5 Rysunek 2. Logarytmiczna charakterystyka modułu i fazy Wartość k obliczyłyśmy ze wzoru 20 log k= Lm Wartość T obliczyłam ze wzoru T= 1/ w, gdzie w jest wartością odczytaną z wykresu (w= 0.073) natomiast wartość k obliczyłam ze wzoru 20 log k= Lm Obliczenia: T= 1/w= 1/ 0.073= 13.698 Lm= 20 log k 10.2= 20 log k log k= 0.477 k= 100.477 k= 2.991 Rozkład zer i biegunów badanego członu Wyznaczenie wartości zer i biegunów, a następnie porównanie z wartościami pomierzonymi: s s s G 9 . 0 12 7 . 2 ) ( 2 + = Bieguny: przyrównujemy mianownik transmitancji do zera: 075 . 0 ) 12 /( 9 . 0 12 0 9 . 0 12 2 2 − = − = = + s s s s s s Biegun wyliczony jak i odczytany są takie same -0.075 Następnie sprowadzamy transmitancję do postaci: G(s)= k/ (1+ sT) Stąd: k=3, a T=13.3 - 0 . 0 8 - 0 . 0 7 5 - 0 . 0 7 - 0 . 0 6 - 0 . 0 5 - 0 . 0 4 - 0 . 0 3 - 0 . 0 2 - 0 . 0 1 0 - 1 - 0 . 8 - 0 . 6 - 0 . 4 - 0 . 2 0 0 . 2 0 . 4 0 . 6 0 . 8 1 b i e g u n s = - 0 . 0 7 5 Tabela dokładności: TRANSMITANCJA BADANEGO OBIEKTU PARAMETR 1 PARAMETR 2 G(s)= 4.2/(16s+1.3) k T Pomiar ch-ki czasowej 3 13.3 Pomiar ch-ki amplitudowej 3.006 12.03 Pomiar ch-ki fazowej
(…)
… odpowiednio zakwalifikować
badany człon ( np. inercyjny różniczkujący itp.) i o ile to możliwe odtworzyć jego
transmitancję. Na jej podstawie możemy przystąpić do badań laboratoryjnych nie narażając
się na kosztowne próby na obiekcie rzeczywistym. Jednak wyniki otrzymane z charakterystyk
minimalnie różnią się od tych obliczonych z transmitancji. Błędy te są spowodowane
trudnością przyłożenia idealnej asymptoty równoległej do funkcji ,oraz rozdzielczością
przedstawianych wykresów. Oczywiście duży wpływ na wyniki ma też staranność
wykonującego odczyty.
…
... zobacz całą notatkę






Komentarze użytkowników (0)