To tylko jedna z 26 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


ZASADY ZACHOWANIA W MECHANICE PŁYNÓW
ZASTOSOWANIA RÓWNANIA BERNOULLIEGO
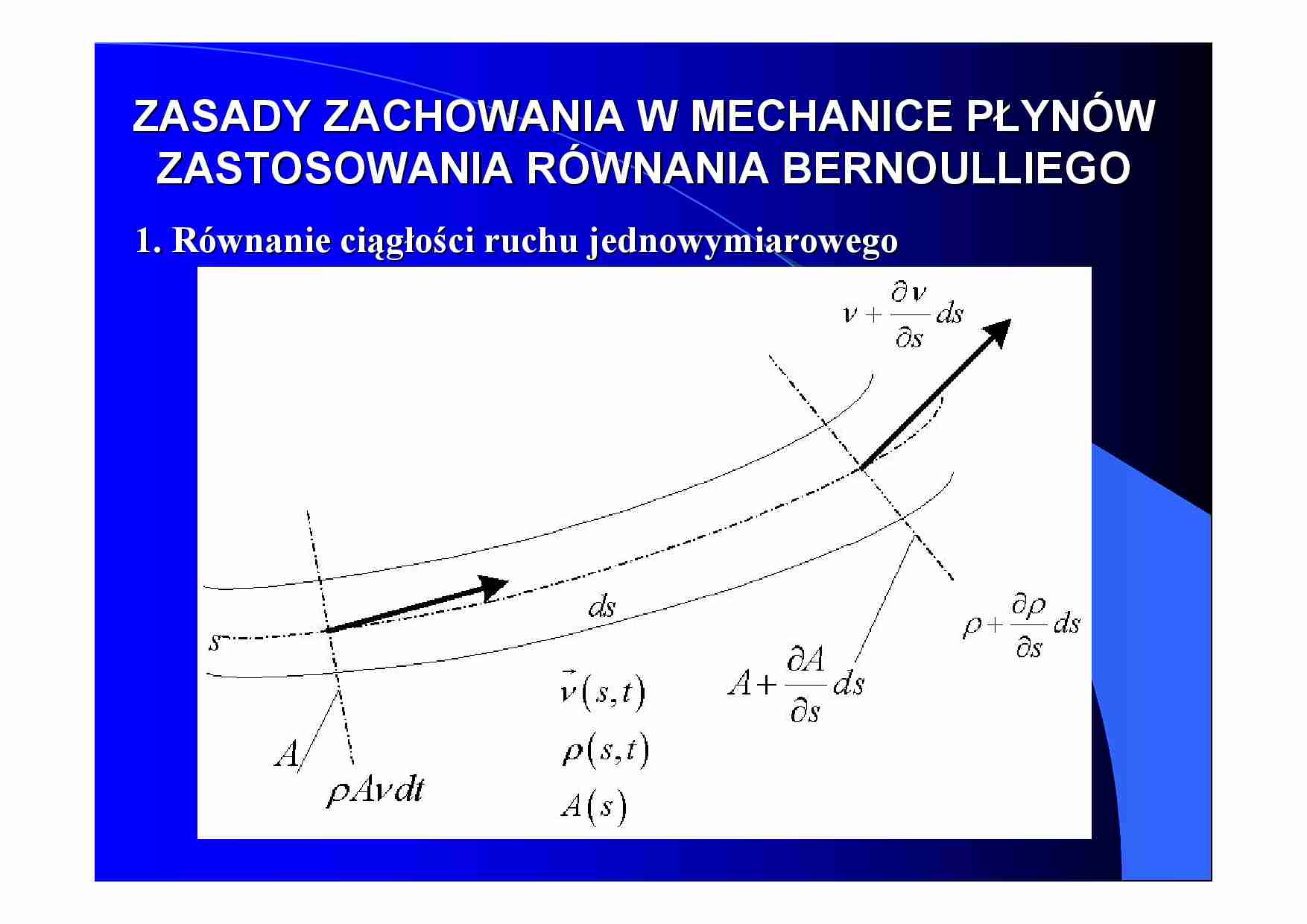
1. Równanie ciągłości ruchu jednowymiarowego
Masa płynu wpływającego w czasie dt przez przekrój 1-1 wynosi ρ Aν dt ,
a wypływającego przez przekrój 2-2:
∂p ⎞ ⎛
∂A ⎞ ⎛
∂ν
⎛
⎞
ρ+
ds ⎟ ⎜ A +
ds ⎟ ⎜ν +
ds ⎟ dt
⎜
∂s
∂s
∂s
⎝
⎠⎝
⎠⎝
⎠
(1)
Po wymnożeniu i pominięciu wielkości małych wyższego rzędu otrzymamy:
∂A
∂p
∂ν ⎞
⎛
ρν Adt ⎜ ρν
+ Aν
+ Aρ
⎟ dsdt
∂s
∂s
∂s ⎠
⎝
(2)
W ruchu ustalonym masy płynu przepływającego w czasie dt przez przekrój
1-2 i 2-2 są jednakowe, zatem
∂A
∂p
∂ν ⎞
⎛
ρν Adt = ρν Adt + ⎜ ρν
+ Aν
+ Aρ
⎟ dsdt
∂s
∂s
∂s ⎠
⎝
czyli
∂ ( ρν A )
∂s
= 0 ⇒ ρν A = const
(3)
(4)
W ruchu nieustalonym różnica płynu dopływającego przekrojem 1-1 i
wypływającego przekrojem 2-2 w czasie dt jest równa zmianie masy zawartej
między przekrojami 1-1 i 2-2, będącej skutkiem zmiany gęstości płynu i wynosi:
∂ ( ρν A )
∂ρ
Adsdt = −
dsdt
∂t
∂s
∂ρ ∂ ( ρν A )
A
+
=0
∂t
∂s
czyli
(5)
(6)
Dla ruchu ustalonego
∂ ( ρν A )
∂ρ
=0⇒
= 0 ⇒ ρν A = const
∂t
∂s
Dla płynu nieściśliwego ρ = const , więc ν A = const .
(7)
2. Równanie ciągłości ruchu ogólnego
Różnica mas wpływających i wypływających wynosi:
⎡
∂ ( ρν x ) ⎤
∂ ( ρν x )
dx ⎥ dydzdt = −
dxdydzdt
ρν xdydzdt − ⎢ ρν x +
∂x
∂x
⎢
⎥
⎣
⎦
(
)
(
)
⎡
⎤
∂ ρν y
∂ ρν y
dy ⎥ dxdzdt = −
dxdydzdt
ρν ydxdzdt − ⎢ ρν y +
∂y
∂y
⎢
⎥
⎣
⎦
⎡
∂ ( ρν z ) ⎤
∂ ( ρν z )
dz ⎥ dxdydt = −
dxdydzdt
ρν zdxdydt − ⎢ ρν z +
∂z
∂z
⎢
⎥
⎣
⎦
(8)
(9)
(10)
Suma tych przyrostów jest równa lokalnej zmianie masy wynikającej ze zmiany
gęstości
−
∂ ( ρν x )
∂x
∂ρ
dxdydzdt ,czyli:
∂t
dxdydzdt −
(
∂ ρν y
∂y
) dxdydzdt − ∂ ( ρν ) dxdydzdt = ∂ρ dxdydzdt
z
∂z
Po podzieleniu przez dxdydzdt otrzymamy:
∂ρ
+ div ρν = 0
∂t
( )
∂t
(12)
Po przekształceniach:
∂ρ
+ ν gradρ + ρ divν =
∂t
⎛ ∂ρ
∂ρ
∂ρ
∂ρ ⎞
ν
ν
+ i x + j y + kν z ⎜ i
+j
+k
⎟ + ρ divν =
∂t
∂y
∂z ⎠
⎝ ∂x
(
)
∂ρ ∂ρ
∂ρ
∂ρ
dρ
νx +
νy +
ν z + ρ divν =
+
+ ρ divν
∂t ∂x
∂y
∂z
dt
Więc równanie (12) można zapisać w postaci
dρ
+ ρ divν = 0
dt
(13)
Dla płynu nieściśliwego ρ = const , otrzymamy równanie ciągłości w
postaci
divν = 0
lub
∂ν x ∂ν y ∂ν z
+
+
=0
∂x
∂y
∂z
(14)
(15)
3. Równanie Bernoulliego
Założenia: płyn nielepki, nieściśliwy, ruch jednowymiarowy, ustalony,
prędkość jest stała w przekroju poprzecznym strugi.
Wydzielimy odcinek strugi zawarty między przekrojami 1-1 i 2-2, określimy
energię mechaniczną cieczy w czasie dt. W czasie dt ciecz z przekroju 1-1
przemieści się o ds1 = ν 1dt , a zatem przekrój 2-2 o ds2 = ν 2dt . Całkowita energia
mechaniczna płynu przepływającego przez przekrój 1-1 w czasie dt składa się z:
'
• energii potencjalnej położenia Ep = ρ gQdtz1 ,
• energii potencjalnej ciśnienia, równej iloczynowi siły powierzchniowej p1A1
''
i przesunięcia ds1 = ν 1dt , czyli Ep = p1A1ν 1dt = p1Qdt ,
• energii kinetycznej masy dm = pQdt , poruszającej się z prędkością ν 1 ,
czyli
2
ν1
Ek = ρ Qdt .
2
Całkowita energia przepływająca w czasie dt przez przekrój 1-1 wynosi
Ec1 = ρ gQz1dt + p1Qdt
(…)
…)
Po przekształceniu
v2
p1 = p∞ + ρ ∞ ⇒ v∞ =
2g
2 (p1 − p2 )
ρ
gdzie:
p∞ - ciśnienie statyczne, ps
v2
ρ ∞ - ciśnienie dynamiczne,pd
2g
v2
p1 = p∞ + ρ ∞ - ciśnienie całkowite,pc
2g
zatem:
pc = p s + p d
,
(23)
4.2. Rurka Pitota
h
ρ
ν∞
1
z
p. p.
p∞
1
Z równania Bernoulliego:
p ∞ v2
p1
∞
+
=
.
ρ g 2g ρ g
(24)
Po podstawieniu: p1 = pb + ρ g ( z + h) , p∞ = pb + ρ gz, otrzymamy
pb + ρ g ( z + h)
pb + ρ gz v2
∞
,
+
=
ρg
2g
ρg
a po uproszczeniu
2
ν∞
2g
= h ⇒ ν ∞ = 2gh
(25)
4.3. Rurka Pitota + U-rurka – pomiar prędkości przepływu gazu
Z równania Bernoulliego:
p ∞ v2
p
+ ∞ = 1.
ρ g 2g ρ g
(26)
Z prawa naczyń połączonych, przy założeniu ρm << ρ otrzymamy
v2
pb + ρ ∞ = pb + ∆zρmg,
2g
(27)
skąd
ρm
ν ∞ = 2g∆z .
ρ
(28)
4.4. Rurka Prandtla
Z równania Bernoulliego dla punktu spiętrzania:
ν∞ = 2
p1 − p∞
ρ
.
(29)
Z prawa naczyń…
…
⎝ A1 ⎠
(33)
gdzie: m = A2 jest modułem zwężki.
A1
Po podstawieniu (33) do (32) otrzymamy:
ν2 =
p − p2
1
=
2 1
2
ρ
1−m
2∆p
1
2
1−m
ρ
(34)
Z prawa naczyń połączonych
p1 − p2 = 2g∆z ( ρm − ρ ) g.
(35)
Po podstawieniu (35) do (34) otrzymamy wzór na prędkość
ν2 =
⎛ρ
⎞
1
2g∆z ⎜ m − 1 ⎟ ,
1 − m2
⎝ ρ
⎠
(36)
A po podstawieniu (36) do wzoru qv = ν 2 A2 ,otrzymamy zwór na strumień
przepływu
q2 = A2
⎛ρ
⎞
1
2g…
... zobacz całą notatkę






Komentarze użytkowników (0)