To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


WYKŁAD 8_2
Właściwości koligatywne
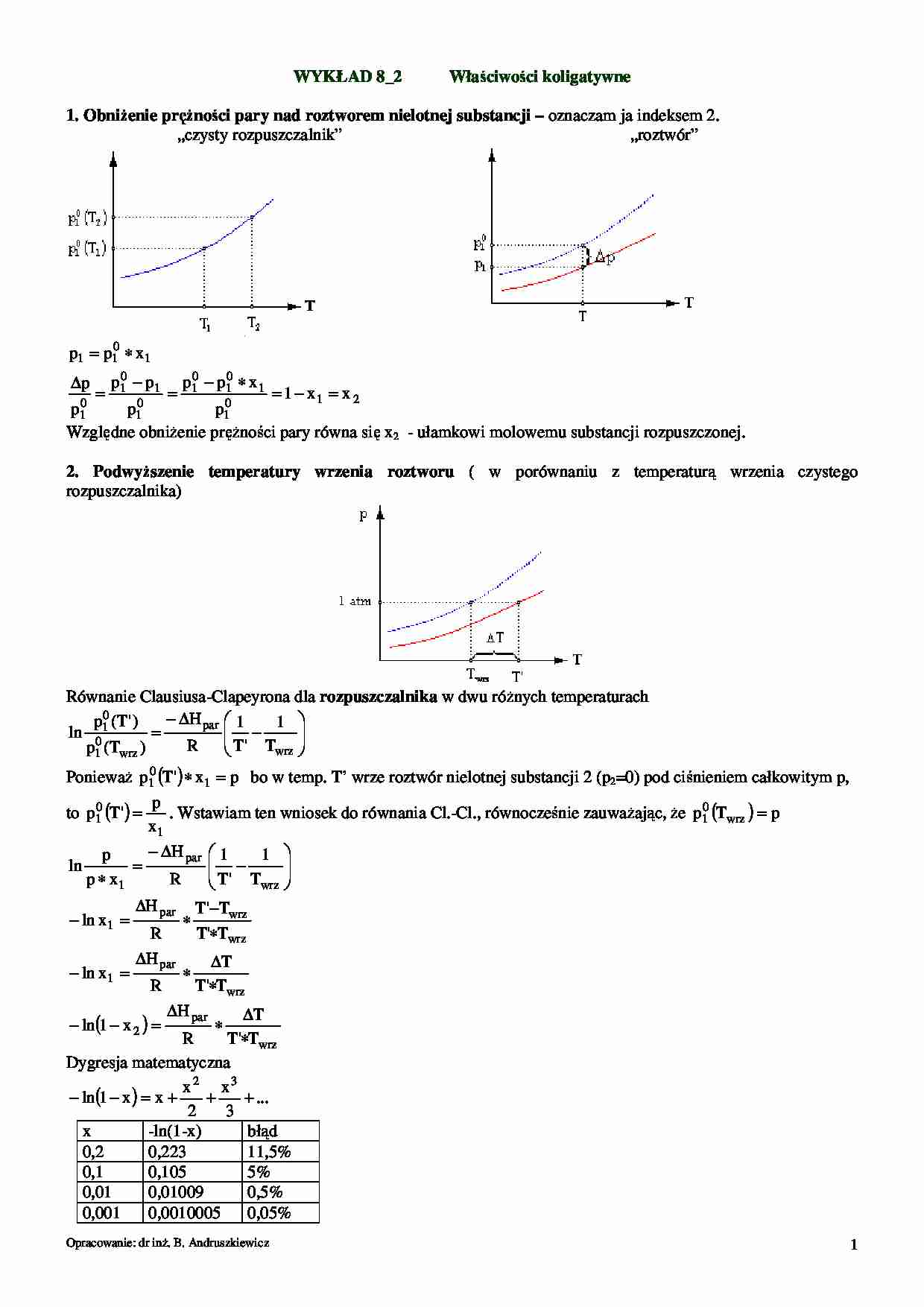
1. ObniŜenie pręŜności pary nad roztworem nielotnej substancji – oznaczam ja indeksem 2.
„czysty rozpuszczalnik”
„roztwór”
0
p 1 = p1 ∗ x 1
∆p
=
0
p1 − p1
=
0
0
p1 − p1 ∗ x 1
= 1 − x1 = x 2
0
0
0
p1
p1
p1
Względne obniŜenie pręŜności pary równa się x2 - ułamkowi molowemu substancji rozpuszczonej.
2. PodwyŜszenie temperatury wrzenia roztworu ( w porównaniu z temperaturą wrzenia czystego
rozpuszczalnika)
Równanie Clausiusa-Clapeyrona dla rozpuszczalnika w dwu róŜnych temperaturach
− ∆H par 1
p 0 (T ' )
1
−
=
ln 01
T' T
R
p1 (Twrz )
wrz
0
PoniewaŜ p1 (T ') ∗ x 1 = p bo w temp. T’ wrze roztwór nielotnej substancji 2 (p2=0) pod ciśnieniem całkowitym p,
p
0
0
to p1 (T') =
. Wstawiam ten wniosek do równania Cl.-Cl., równocześnie zauwaŜając, Ŝe p1 (Twrz ) = p
x1
− ∆H par 1
p
1
−
ln
=
T' T
p ∗ x1
R
wrz
∆H par T '−Twrz
− ln x 1 =
∗
R
T '∗Twrz
∆H par
∆T
− ln x 1 =
∗
R
T '∗Twrz
∆H par
∆T
− ln(1 − x 2 ) =
∗
R
T '∗Twrz
Dygresja matematyczna
x2 x3
− ln(1 − x ) = x +
+
+ ...
2
3
x
-ln(1-x)
błąd
0,2
0,223
11,5%
0,1
0,105
5%
0,01
0,01009
0,5%
0,001
0,0010005
0,05%
Opracowanie: dr inŜ. B. Andruszkiewicz
1
Wniosek: dla małych wartości x wyraŜenie –ln(1-x) równa się x. Koniec dygresji.
∆H par ∆T
∆H par
∆T
∗ 2
Wracając do równania Cl.-Cl.: x 2 =
i dalej przybl. x 2 =
∗
R
R
T '∗Twrz
Twrz
Weźmy 1000g rozpuszczalnika i m moli substancji 2
∆H par ∆T
mM1
mM1
m
m
x2 =
≈
=
czyli
=
∗ 2
stąd
1000g / kg 1000g / kg 1000g / kg
1000g / kg
R
Twrz
m+
M1
M1
2
Twrz temp.wrzenia rozpuszczalnika pod ciśn.1atm w K
RTwrz ∗ M1
∆T =
∗m
M1 masa molowa rozpuszczalnika w g/mol
∆H par ∗ 1000g / kg
∆Hpar entalpia parowania rozpuszczalnika w J/mol
m stęŜenie molalne substancji nielotnej w molach/kg
rozpuszczalnika.
Oznaczając przez E
K ∗ kg
ułamek charakteryzujący rozpuszczalnik ( stała ebulioskopowa mierzona w
) otrzymuję ∆T = E ∗ m
mol
PodwyŜszenie temperatury wrzenia roztworu nie zaleŜy od tego, jakie cząstki znajdują się w roztworze
(oprócz rozpuszczalnika), tylko ile ich jest.
Przykłady
1.Rozpuszczono 1 mol NaCl w wodzie. Ile moli cząstek (poza rozpuszczalnikiem) jest w roztworze? Jakie to
cząstki? 1mol jonów Na+ i 1 mol jonów Cl-, razem 2 mole.
2.Rozpuszczono 1 mol Na2SO4 w wodzie. Ile moli cząstek (poza rozpuszczalnikiem) jest w roztworze? Jakie to
cząstki? 2mole jonów Na+ i 1mol jonów SO 2− , razem 3mole
4
3.Rozpuszczono 1 mol kwasu octowego w wodzie. Kwas ten zdysocjował na jony w 30%. Ile moli cząstek (poza
rozpuszczalnikiem) jest w roztworze? Jakie to cząstki? 0,7mola niezdysocjowanych cząsteczek kwasu octowego,
0,3 mola jonów H+ i 0,3 mola jonów CH3COO-, razem 1,3 mola róŜnych indywiduów chemicznych.
3. ObniŜenie temperatury krzepnięcia roztworu
(w porównaniu z temperaturą krzepnięcia czystego rozpuszczalnika)
∆H top1 1
∆H top1 1
1
1
− czyli ln(1 − x 2 ) =
−
Ttop1 T '
Ttop1 T '
R
R
∆H top1 T '−Ttop1
ln (1 − x 2 ) =
∗
R
Ttop1 ∗ T '
ln x 1 =
a zmieniając znak: − ln (1 − x 2
(…)
… mierzona w
K ∗ kg
) otrzymuję
mol
∆T = K ∗ m
ObniŜenie temperatury krzepnięcia roztworu nie zaleŜy od tego, jakie cząstki znajdują się w roztworze
(oprócz rozpuszczalnika), tylko ile ich jest.
Opracowanie: dr inŜ. B. Andruszkiewicz
2
4. Zjawiska 3, 4, 5 oraz pominięte tutaj ciśnienie osmotyczne to zjawiska koligatywne (spokrewnione ).
Efekty tych zjawisk (obserwowane ∆p, ∆Twrz, ∆Tkrz, π)
są miarą ilości…
... zobacz całą notatkę






Komentarze użytkowników (0)