To tylko jedna z 17 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


STATYKA PŁYNÓW-NAPORY
1. Powtórka
Równanie Eulera hydrostatyki
q=
1
grad p
ρ
X=
1 ∂p
ρ ∂x
1 ∂p
Y=
ρ ∂y
Z=
(1)
(2)
1 ∂p
ρ ∂z
W płynie znajdującym się stanie spoczynku reakcją na działanie sił masowych
(ciężkości, bezwładności) oraz powierzchniowych (np. nacisk tłoka)
jest powstanie pola ciśnień.
Ciśnienie definiujemy w postaci:
p = lim
∆A→0
Rodzaje ciśnień
bezwzględne – określane względem próżni
względne
• nadciśnienie pn = pa 2 − pb
• podciśnienie p p = pb − pa1
∆P
∆A
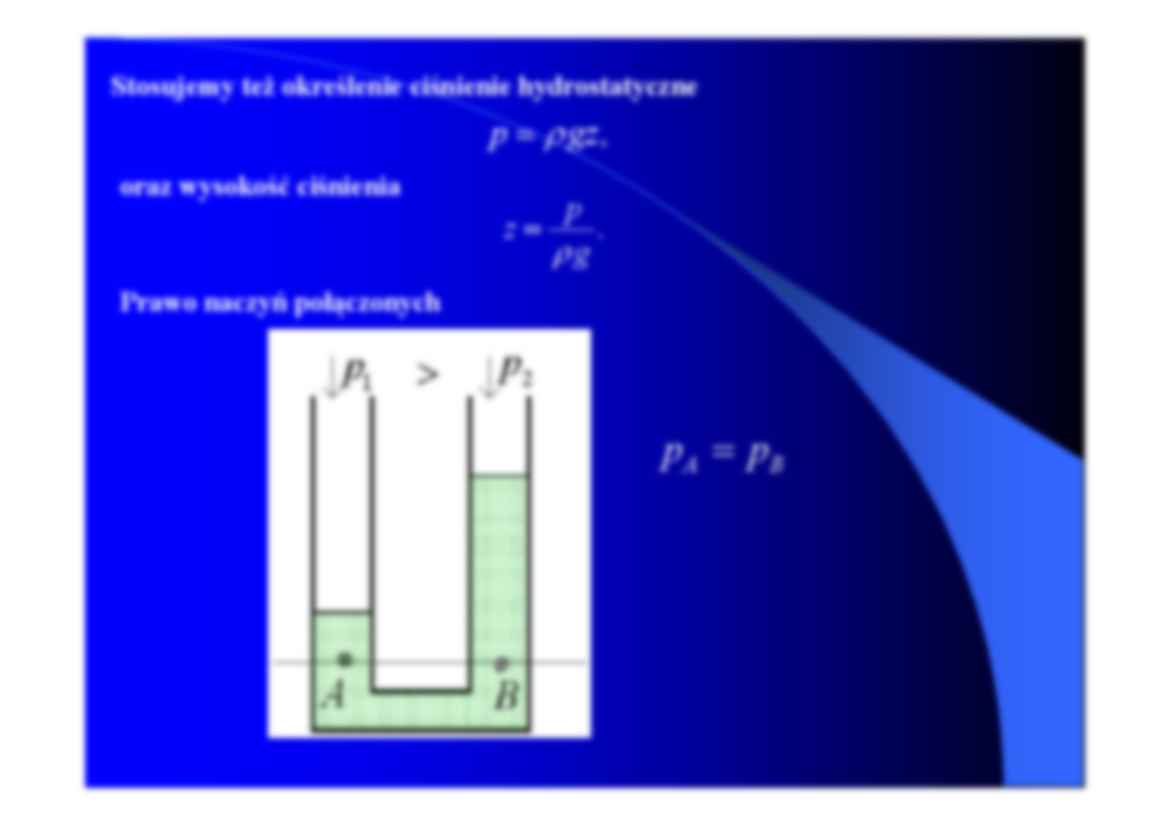
Stosujemy też określenie ciśnienie hydrostatyczne
p = ρ gz ,
oraz wysokość ciśnienia
z=
p
.
ρg
Prawo naczyń połączonych
p A = pB
2. Napór na ścianę płaską
α
S
Σ
Należy wyznaczyć wektor naporu wypadkowego N , to znaczy:
- moduł wektora naporu N
dN = ρ dA
(4)
N = ∫ ρ dA
(5)
A
- kierunek naporu wypadkowego: jest zawsze prostopadły do ściany
- punkt przyłożenia (środek naporu) Σ ( xΣ , yΣ )
Moduł wektora naporu N wyznaczamy ze wzoru (5) po podstawieniu
p = ρ gz i obliczeniu całki po powierzchni A:
N = ∫ ρ gzdA =ρ gzs A,
A
ponieważ
(6)
∫ zdA =z A,
s
A
gdzie: A jest polem powierzchni zwilżonej części ściany, a zs głębokością
zanurzenia jej środka geometrycznego.
Moduł wektora naporu hydrostatycznego na ścianę płaską o dowolnym
konturze i dowolnym nachyleniu jest równy ciężarowi słupa cieczy,
którego podstawą jest zanurzona część ściany a wysokością głębokość
zanurzenia środka ciężkości. Z tego spostrzeżenia wynika paradoks
hydrostatyczny Stevina
N = ρ ghA
(7)
h
A
A
A
A
Środek naporu
Moment naporu wypadkowego względem osi OX wynosi
NyΣ = ∫ ρ gzdAy
(8)
A
Po podstawieniu
z = y sin α , N = ρ gzs A = ρ gys sin α A
(9)
Otrzymamy współrzędną yΣ środka naporu w postaci
yΣ =
∫ ρ gzdAy
A
N
ρ g sin α ∫ y 2 dA
y 2 dA
∫
Ix
=
=
=
ρ g sin α ys A
ys A
Mx
A
A
(10)
Z twierdzenia Steinera
I x = I s + Ay
zatem
2
s
(11)
I s + Ays2
Is
yΣ =
= ys +
Ays
ys A
(12)
Po podstawieniu
z∑
yΣ =
,
sin α
otrzymamy
zs
ys =
,
sin α
z∑
z∑
Is
=
+
sin α sin α A zs
sin α
(13)
(14)
Po obustronnym pomnożeniu równania (14) przez sin α otrzymamy
Is
sin α 2
z∑ = z s +
zs A
(15)
Dla ściany pionowej ( α = 90° ,sin α = 1 ) o szerokości b i wysokości h
Is
h bh3 h h 2
z∑ = z s +
= +
= + = h
zs A 2 12 2 6 3
3. Napór na ścianę zakrzywioną
x
Az
sz
y
Ax
sx
s
sy
Ay
A
z
W przypadku ściany zakrzywionej wyznaczamy zwykle składowe poziome
i pionowe naporu. Składowe poziome wyznaczamy jako napory na ściany płaskie
powstałe w wyniku rzutowania ściany zakrzywionej na płaszczyzny prostopadłe
do osi poziomych. Składowa pionowa naporu jest równa ciężarowi cieczy zawartej
pomiędzy zakrzywioną powierzchnią, zwierciadłem cieczy i płaszczyznami
pionowymi ograniczającymi powierzchnię zakrzywioną.
N x = ρ gzsz Ax
N y = ρ gzsy Ay
N z = ρ gV
(16)
W przypadku ściany symetrycznej.
1
1
2
N z = ρ gV = ρ g π R L = πρ gR 2 L
4
4
1
1
N x = ρ gzsz Ax = ρ g RRL = ρ gR 2 L
2
2
(17)
N = N x2 + N z2 ,
1
πρ gR 2 L 1
Nz 4
tgα =
=
= π
N x 1 πρ gR 2 L 8
2
Współrzędne
... zobacz całą notatkę






Komentarze użytkowników (0)