To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę

Przestrzenie sygnałów
Dziedzina czasu, dziedzina częstotliwości
W dziedzinie ciągłej
W dziedzinie dyskretnej
x n=... X f , X , =2 f /F s
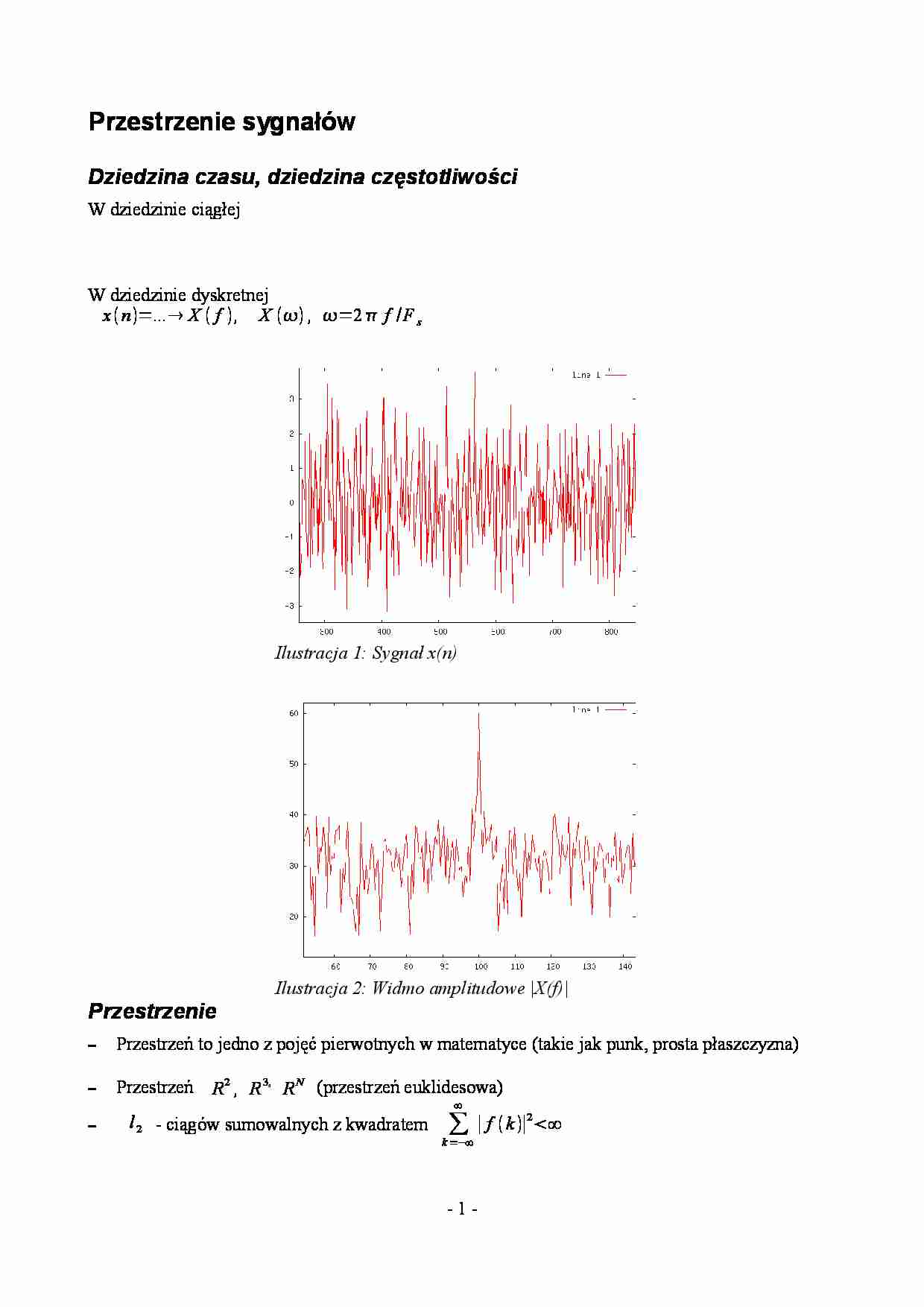
Ilustracja 1: Sygnał x(n)
Ilustracja 2: Widmo amplitudowe |X(f)|
Przestrzenie
–
Przestrzeń to jedno z pojęć pierwotnych w matematyce (takie jak punk, prosta płaszczyzna)
–
Przestrzeń
R2 , R 3, RN (przestrzeń euklidesowa)
∞
–
l 2 - ciągów sumowalnych z kwadratem
∑ ∣ f k ∣2∞
k =−∞
-1-
∞
L 2 −∞ , ∞ - funkcji całkowalnych z kwadratem
–
∫ ∣ f t ∣2 dt∞
−∞
T
L 2 0,T - funkcji całkowalnych z kwadratem w przedziale (0,T)
–
∫∣ f n∣2 dn∞
0
–
Nazwa przestrzenie wskazuje na to czym są elementy zbioru oraz jakie operacje matematyczne
są zdefiniowane. Np. przestrzenie wektorowe definiują:
– iloczyn skalarny,
A=a 0, a1, a 2, ... , a N −1 , B=b0, b 1, b2, ... , b N −1
wymagane własności:
1) A ° B= B° A
2) A B°C= A°CB °C
3) x∗A° B= A° x∗B= x∗ A° B
A ° A0 dla A≠0
4)
A ° A=0 dla A=0
– definicja iloczynu
N −1
N −1
A° B=∑ n=0 a n bn=∑ n=0 b n an =B ° A
A° B= A B
–
T
norma wektora (przestrzeń unormowana)
∥ A∥= A° A= A AT =
–
–
∑n=0 ∣an∣
N −1
metryka indukowana z normy
∥ A−B∥= A−B A−BT =
inne normy
2
∑ ∣a −b ∣
2
n
n
N −1
∥ A∥=∑n=0 ∣a n∣ jaka metryka ? ∥ A−B∥=? ??
∥ A∥= max ∣a n∣ jaka metryka ? ∥ A−B∥=? ??
0 nN
–
inne metryki – taksówkowa
W CPS - przestrzeń Hilberta
zupełna, liniowa, unitarna/unormowana
Liniowa – tzn.:
– dodawanie wektorów
– mnożenie przez skalar
– iloczyn skalarny
– norma
Zupełna – wynik operacji liniowej należy do tej samej przestrzeni liniowej
Unitarna – norma wektorów bazowych =1
-2-
... zobacz całą notatkę




Komentarze użytkowników (0)