Wykład - Przenikanie przez przegrodę płaską

Nasza ocena:

3
Pobrań: 273
Wyświetleń: 1302
Komentarze: 0
Notatek.pl

Pobierz ten dokument za darmo

Pobierz notatkę
Podgląd dokumentu
Wykład - Przenikanie przez przegrodę płaską - strona 1 Wykład - Przenikanie przez przegrodę płaską - strona 2 Wykład - Przenikanie przez przegrodę płaską - strona 3

Fragment notatki:

WYKŁAD 2
1.03.2000
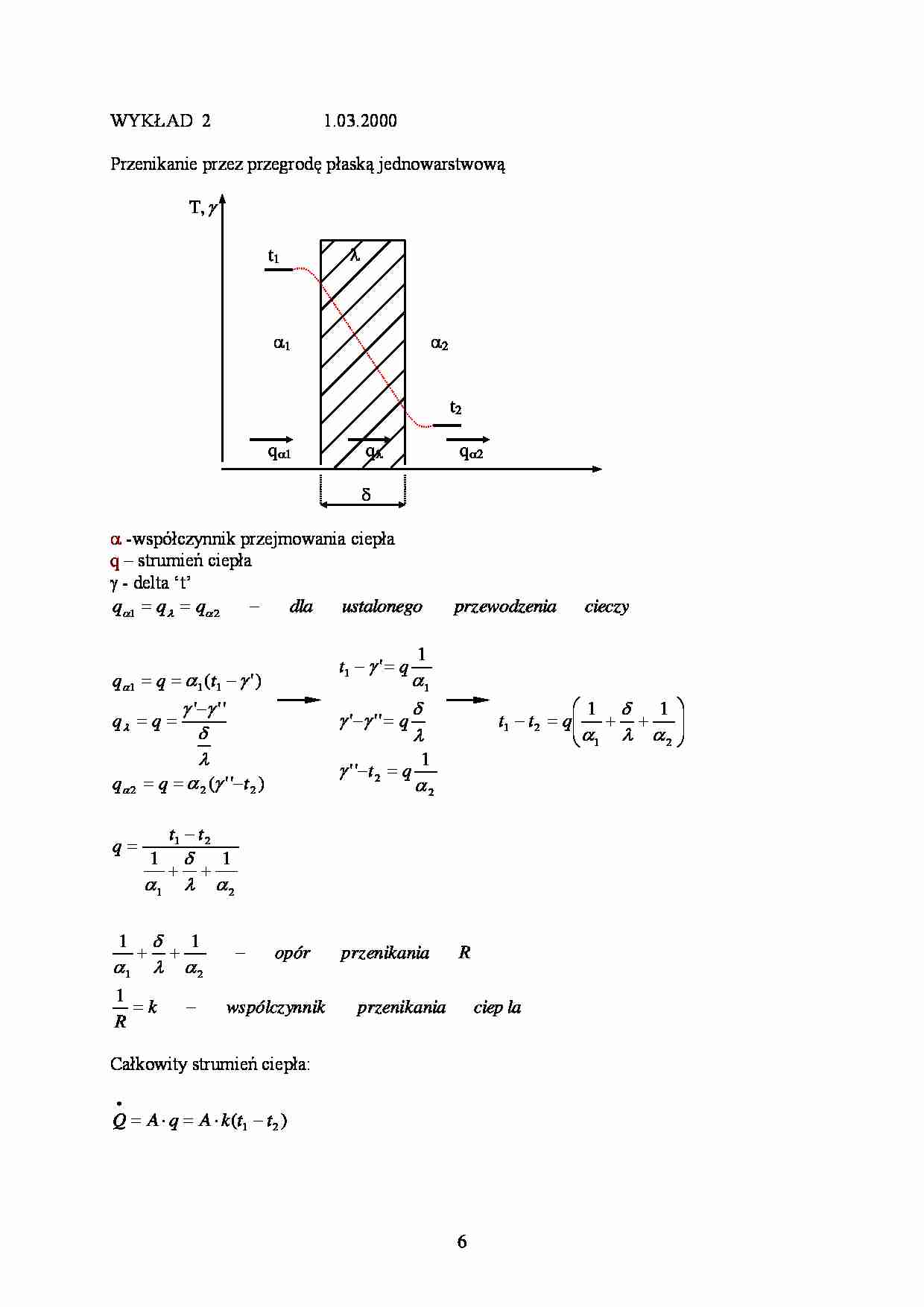
Przenikanie przez przegrodę płaską jednowarstwową
T, 
t1

1
2
t2
q1
q
q2

 -współczynnik przejmowania ciepła
q – strumień ciepła
 - delta ‘t’
q1  q  q 2

dla
ustalonego
t1   '  q
q 1  q   1 (t1   ' )
 ' ' '


 q   2 ( ' 't 2 )
1
1
1
 1 
1 

t1  t 2  q  

 2 
 1

1
2
t1  t 2
q
1
 ' 't 2  q


 1

 2
 1

 2
1
k
R


opór
wspólczynnik
cieczy
1
1

 ' ' '  q

q  q 
q 2
przewodzenia
przenikania
R
przenikania
ciep la
Całkowity strumień ciepła:
*
Q  A  q  A  k (t1  t 2 )
6
Dla ścian wielowarstwowych (pionowych):
q
t1  t 2
1
1
 
   
1 i    i  2
ŚCIANY WIELOWARSTWOWE (POZIOME)
1
A1, 1
A2, 2
2
A3,3
*
*
1  2
  2
  2
; Q 2  A2 1
; Q 3  A3 1



11
2
3
*
*
*
*
  2
Q  Q 1  Q 2  Q 3  ( A11  A2  2  A3 3 ) 1
 calkowity strumień

*
Q 1  A1
przenikający
Lambada zastępcze:
Z 
A11  A2  2  A3 3
A
Na każdej warstwie gęstość strumienia jest inna.
7
ciepa
PRZEGRODA CYLINDRYCZNA (RUROWA)

1

l
2
Rw
r
R
Rz
*
 (r ) ; Q  idem
w
s tan ie
ustalonym
Gęstość strumienia maleje ze wzrostem ‘r’.
*
Q   A(r )  
*
Q  2rl
d
dr
A(r )  2rl
d
dr
*
Q
d
ql   2r
l
dr
dr
ql 
 2 d
r
calkujemy :
ql ln r  2  C
 - jest zależna logarytmicznie od promienia ‘r’
Warunki brzegowe:
1. r = rw
2. r = rz
 = 1
 = 2
8
ql ln rw  2 1  C
(1)
ql ln rz  2 2  C
ql ln
rz
 ( 1   2 )
 2 ( 1   2 )  ql 
r
rw
ln z
rw
2
ŚCIANA CYLINDRYCZNA WIELOWARSTWOWA

1 2 3
r
ql 
 ( 1   2 )
 dz
 ln
d
  2 w

i







i
9
Dwa płyny przedzielone przegrodą cylindryczną

t1

ql
1
2
ql
t2
ql
Rw
r
Rz
 (t1   ' )  ql
ql  d w 1 (t1   ' )
ql 
d w 1
dz
dw
2
1
ln
 ( ' ' ' )
 ( ' ' ' )  ql
d
ln z
dw
2
ql  d z 2 ( ' 't 2 )
 ( ' 't 2 )  ql
d

ln z

dw
1
1
 (t1  t 2 )  ql 


d 
2
d z 2
 w 1

ql 
1
 (t1  t 2 )
d
ln z
dw
1
1


d w 1
2
d z 2
d z 2






 przenikanie
ciepla
Dla przegrody wielowarstwowej cylindrycznej:
ql 
 (t1  t 2 )
 dz
 ln
dw
1
 
 2
d w 1
i


a


  1
 d
z 2

i
10
przez
przegrodę
cylindrycz na
Jeśli wzrośnie promień zewnętrzny przegrody cylindrycznej to przenikalność cieplna może
wzrosnąć.
Średnica krytyczna – średnica, przy której występuje minimalny opór przewodzenia ciepła.
ql R
R(dz)
ql(dz)
dkr – średnica krytyczna
d
Obszar średnic rzeczywistych – nałożenie izolacji
d kr 
w tym obszarze spowoduje wzrost strumienia
ciepła odprowadzanego
PRZEGRODA KULISTA

1
2
Rw Rz
*
Q  idem ;
 (r )  s tan
d
;
dr
*
d
Q  4r 2 
dr
*
Q   A(r )
ustalony
A(r )  4r 2
11
2
2
dr
 4 d
r
* 1
 Q  4  C
r
*
Q
Warunki brzegowe:
1. r = rw
2. r = rz
*
Q
*
Q
 = 1
 = 2
1
 4 1  C
rw
1
 4 2  C (1)
rz
* 1
1
Q    4 ( 1   2 )
r

 w ... zobacz całą notatkę



Komentarze użytkowników (0)

Zaloguj się, aby dodać komentarz