To tylko jedna z 6 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


1. POJĘCIA PODSTAWOWE
14
Oznaczenia
Symbol
Oznacza
Przykład
wielka litera alfabetu łacińskiego
cyfra arabska
cyfra rzymska
punkt dany
punkt pomocniczy
punkt wynikowy
A, B, X, Y
1, 2, 3
I, II, III
mała litera alfabetu łacińskiego
prosta lub krzywa
prosta pozioma
prosta czołowa
a, b, m, y, z
p
f
płaszczyznę (pocz.)
lub kąt (końcowe)
α, β, γ
ω, ϕ, ψ
równoległość
elementów
h||x, a||p
mała litera alfabetu greckiego
||
15
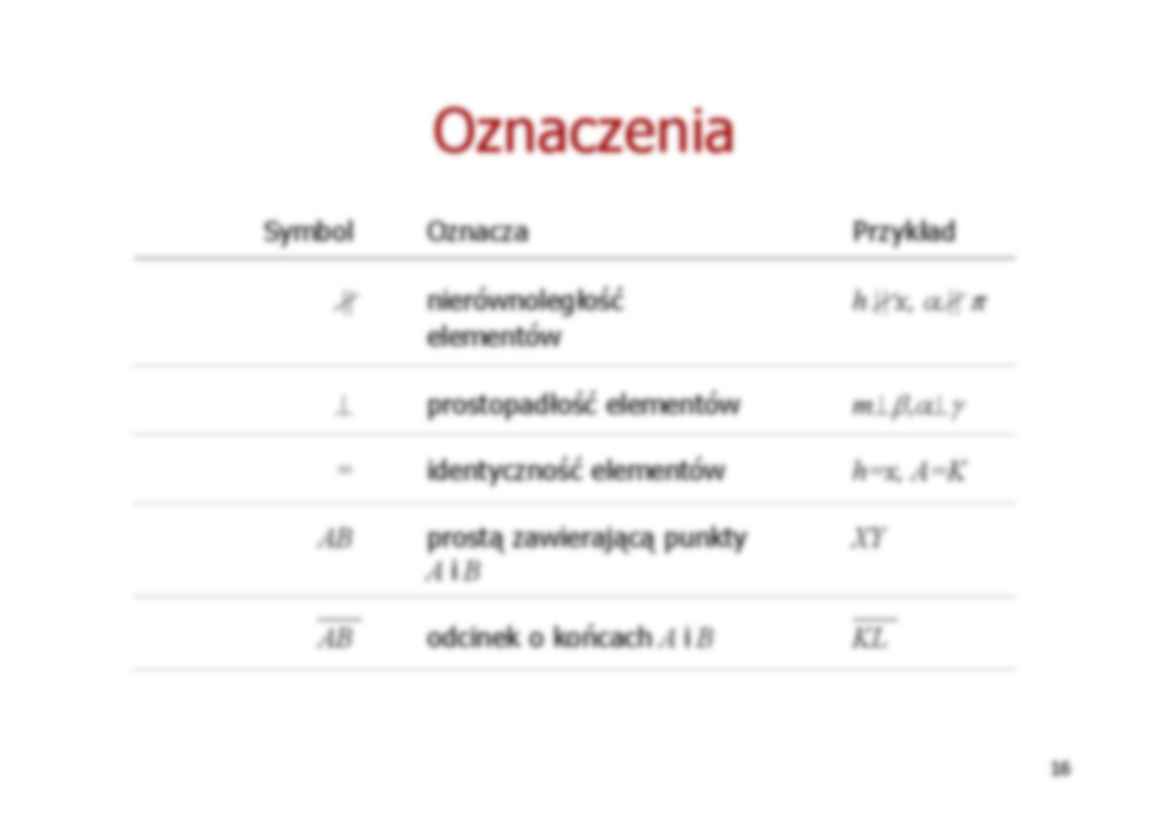
Oznaczenia
Symbol
Oznacza
Przykład
||
nierównoległość
elementów
h || x, α || π
⊥
prostopadłość elementów
m⊥β,α⊥γ
=
identyczność elementów
h=x, A=K
AB
prostą zawierającą punkty
AiB
XY
AB
odcinek o końcach A i B
KL
16
Oznaczenia
Symbol
Oznacza
Przykład
Al (A× l)
płaszczyznę zawierającą
punkt A i prostą l
α = Dm
lm (l×m)
płaszczyznę zawierającą
proste l i m
punkt wspólny prostych l i m
β =xy
mα, αm
(m×α)
αβ (α×β)
A=ab
punkt wspólny prostej m
i płaszczyzny α
X=mα, K=γl
prostą wspólną płaszczyzn
αiβ
q=αβ
17
Podstawowe twierdzenia
i definicje
Def.1
Mówimy, że prosta jest prostopadła do
płaszczyzny jeśli jest prostopadła do każdej
prostej tej płaszczyzny.
Tw.1
Jeśli prosta c jest prostopadła do dwu
przecinających się prostych a i b to jest
prostopadła do każdej prostej leżącej w
płaszczyźnie ab.
18
Podstawowe twierdzenia
i definicje
Tw.2
Każda płaszczyzna przechodząca przez prostą
prostopadłą do pewnej płaszczyzny jest do tej
płaszczyzny prostopadła.
Tw.3
Istnieje tylko jedna płaszczyzna prostopadła do
płaszczyzny α i przechodząca przez
nieprostopadłą do płaszczyzny α prostą m.
19
... zobacz całą notatkę






Komentarze użytkowników (0)