2. CAŁKI KRZYWOLINIOWE ZORIENTOWANE
2.1 DEFINICJE I WŁASNOŚCI CAŁEK KRZYWOLINIOWYCH ZORIENTOWANYCH
Def. 2.1.1 (pole wektorowe na płaszczyźnie i w przestrzeni)
a) Niech D będzie obszarem na płaszczyźnie. Polem wektorowym na D nazywamy funkcję wektorową F : D R 2 , gdzie
F ( x, y) P( x, y), Q( x, y) dla (x,y) D.
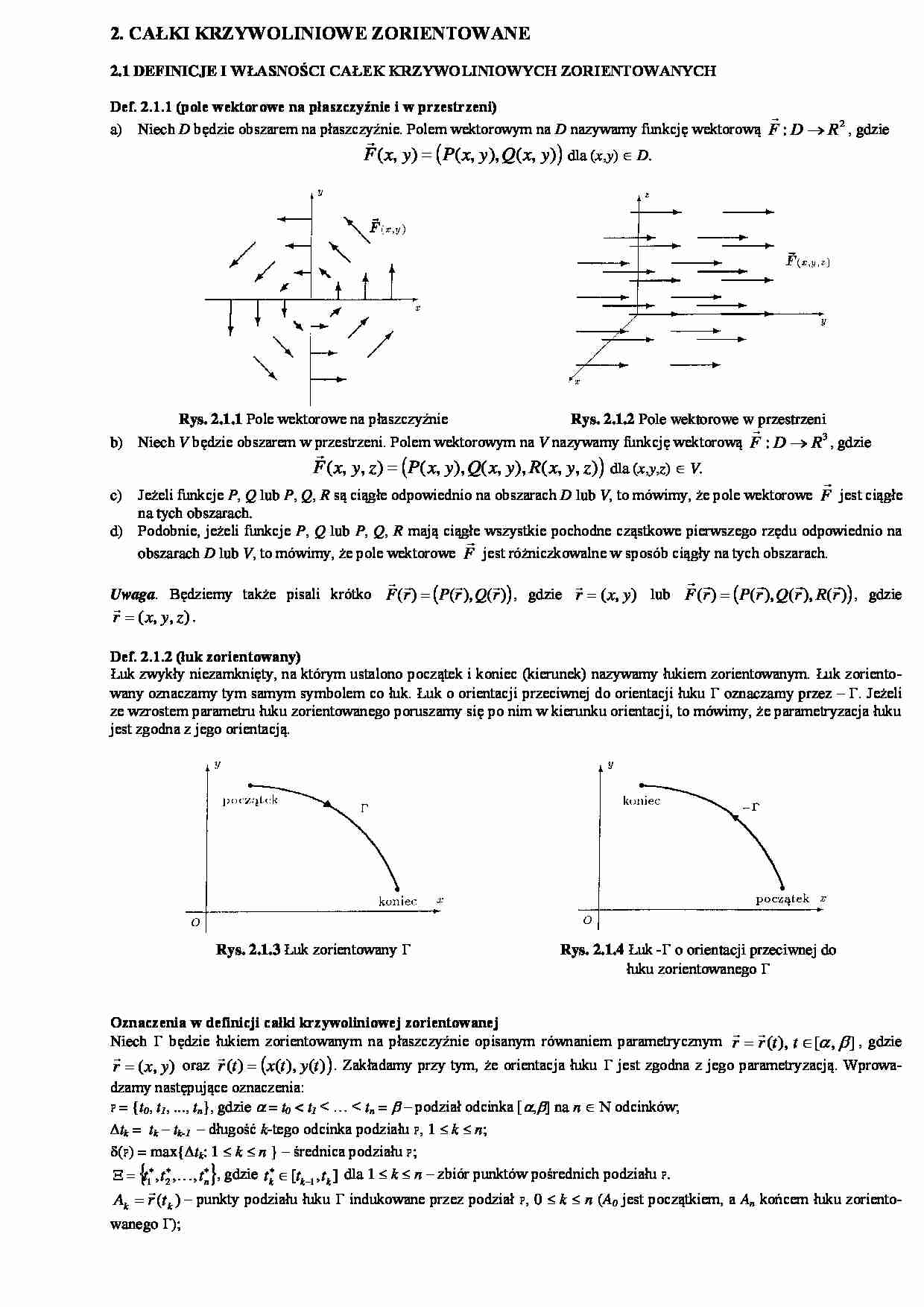
Rys. 2.1.1 Pole wektorowe na płaszczyźnie
Rys. 2.1.2 Pole wektorowe w przestrzeni
b) Niech V będzie obszarem w przestrzeni. Polem wektorowym na V nazywamy funkcję wektorową F : D R3 , gdzie
F ( x, y, z ) P( x, y), Q( x, y), R( x, y, z) dla (x,y,z) V.
Jeżeli funkcje P, Q lub P, Q, R są ciągłe odpowiednio na obszarach D lub V, to mówimy, że pole wektorowe F jest ciągłe
na tych obszarach.
d) Podobnie, jeżeli funkcje P, Q lub P, Q, R mają ciągłe wszystkie pochodne cząstkowe pierwszego rzędu odpowiednio na
obszarach D lub V, to mówimy, że pole wektorowe F jest różniczkowalne w sposób ciągły na tych obszarach.
c)
Uwaga. Będziemy także pisali krótko F (r ) P(r ), Q(r ) , gdzie r ( x, y) lub F (r ) P(r ), Q(r ), R(r ) , gdzie
r ( x, y, z ) .
Def. 2.1.2 (łuk zorientowany)
Łuk zwykły niezamknięty, na którym ustalono początek i koniec (kierunek) nazywamy łukiem zorientowanym. Łuk zorientowany oznaczamy tym samym symbolem co łuk. Łuk o orientacji przeciwnej do orientacji łuku oznaczamy przez – . Jeżeli
ze wzrostem parametru łuku zorientowanego poruszamy się po nim w kierunku orientacji, to mówimy, że parametryzacja łuku
jest zgodna z jego orientacją.
Rys. 2.1.3 Łuk zorientowany
Rys. 2.1.4 Łuk - o orientacji przeciwnej do
łuku zorientowanego
Oznaczenia w definicji całki krzywoliniowej zorientowanej
Niech będzie łukiem zorientowanym na płaszczyźnie opisanym równaniem parametrycznym r r (t ), t [ , ] , gdzie
r ( x, y) oraz r (t ) x(t ), y(t ) . Zakładamy przy tym, że orientacja łuku jest zgodna z jego parametryzacją. Wprowadzamy następujące oznaczenia:
P = {t0, t1, ..., tn}, gdzie = t0
... zobacz całą notatkę





Komentarze użytkowników (0)