1. CAŁKI KRZYWOLINIOWE NIEZORIENTOWANE
1.1 ŁUKI NA PŁASZCZYŹNIE I W PRZESTRZENI
Def. 1.1.1 (funkcja wektorowa jednej zmiennej)
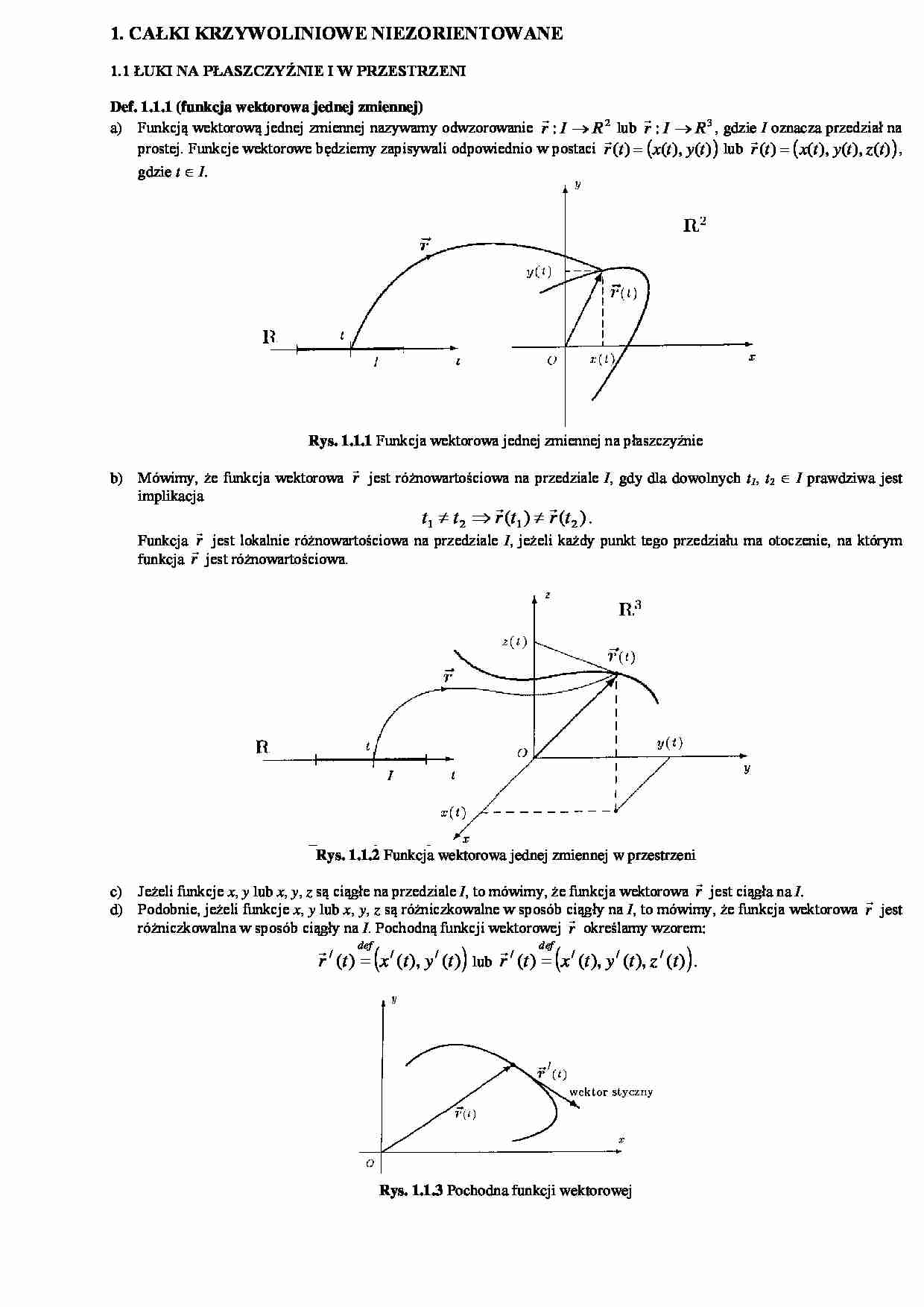
a) Funkcją wektorową jednej zmiennej nazywamy odwzorowanie r : I R 2 lub r : I R 3 , gdzie I oznacza przedział na
prostej. Funkcje wektorowe będziemy zapisywali odpowiednio w postaci r (t ) x(t ), y(t ) lub r (t ) x(t ), y(t ), z (t ) ,
gdzie t I.
Rys. 1.1.1 Funkcja wektorowa jednej zmiennej na płaszczyźnie
b) Mówimy, że funkcja wektorowa r jest różnowartościowa na przedziale I, gdy dla dowolnych t1, t2 I prawdziwa jest
implikacja
t1 t 2 r (t1 ) r (t 2 ) .
Funkcja r jest lokalnie różnowartościowa na przedziale I, jeżeli każdy punkt tego przedziału ma otoczenie, na którym
funkcja r jest różnowartościowa.
Rys. 1.1.2 Funkcja wektorowa jednej zmiennej w przestrzeni
c) Jeżeli funkcje x, y lub x, y, z są ciągłe na przedziale I, to mówimy, że funkcja wektorowa r jest ciągła na I.
d) Podobnie, jeżeli funkcje x, y lub x, y, z są różniczkowalne w sposób ciągły na I, to mówimy, że funkcja wektorowa r jest
różniczkowalna w sposób ciągły na I. Pochodną funkcji wektorowej r określamy wzorem:
def
def
r / (t ) x / (t ), y / (t ) lub r / (t ) x / (t ), y / (t ), z / (t ) .
Rys. 1.1.3 Pochodna funkcji wektorowej
Def. 1.1.2 (łuki na płaszczyźnie)
a) Niech funkcja r : [ , ] R 2 będzie ciągła i różnowartościowa na przedziale [,]. Łukiem zwykłym na płaszczyźnie
nazywamy zbiór:
r (t ) : t [ , ] .
Rys. 1.1.4 Łuk zwykły na płaszczyźnie
b) Niech funkcja r : I R 2 , gdzie I oznacza dowolny odcinek, półprostą lub prostą (z końcem lub nie), będzie ciągła i
lokalnie różnowartościowa na I. Łukiem na płaszczyźnie nazywamy zbiór:
r (t ) : t I .
Rys. 1.1.5 Łuk na płaszczyźnie
c)
Jeżeli dla łuku r (t ) : t [ , ] spełniona jest równość r ( ) r ( ) , to mówimy, że łuk ten jest zamknięty. W
przeciwnym przypadku mówimy, że łuk jest niezamknięty.
Rys. 1.1.6 Łuk zamknięty na płaszczyźnie
d) Jeżeli funkcja r w definicji łuku zwykłego jest różniczkowalna w sposób ciągły na [ ,] oraz dla każdego t [,] spełniony jest warunek:
r (t ) O ,
to mówimy, że łuk ten jest gładki. Mówimy, że łuk jest kawałkami gładki, jeżeli można go podzielić na skończoną liczbę
łuków gładkich.
Rys. 1.1.7 Łuk kawałkami gładki na płaszczyźnie
Uwaga. Podobnie definiuje się łuki analogicznych rodzajów w przestrzeni. Funkcję wektorową r lub funkcje x, y, z opisujące
łuk nazywamy jego parametryzacją. Obrazowo łuk zwykły można przedstawić jako powyginany odcinek ma płaszczyźnie
lub w przestrzeni. Wyginany odcinek można wydłużać lub skracać, ale nie wolno go rozrywać ani sklejać.
Fakt 1.1.3 (o przedstawianiu łuków na płaszczyźnie i w przestrzeni)
Łukami na płaszczyźnie są wykresy funkcji ciągłych postaci:
1. : y = y(x), a x b,
2. : x = x(y), c y d.
Łukami w przestrzeni są części wspólne ciągłych powierzchni walcowych:
... zobacz całą notatkę





Komentarze użytkowników (0)