To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę

Wykład 10. Stateczność prętów. Wyboczenie sprężysto - plastyczne.
Załóżmy, że siła normalna w pręcie jest tak duża, że część przekroju uplastycznia się.
Dokładniej przebieg wyboczenia wyobrażamy sobie następująco: Pod działaniem siły osiowej
przed utratą osiowej postaci ściskania w przekroju panuje naprężenie s0 nie przekraczające
granicy proporcjonalności. W chwili utraty osiowej postaci zginania pojawia się moment
zginający, który, dodając naprężenia w części ściskanej przekroju sprawia, że granica
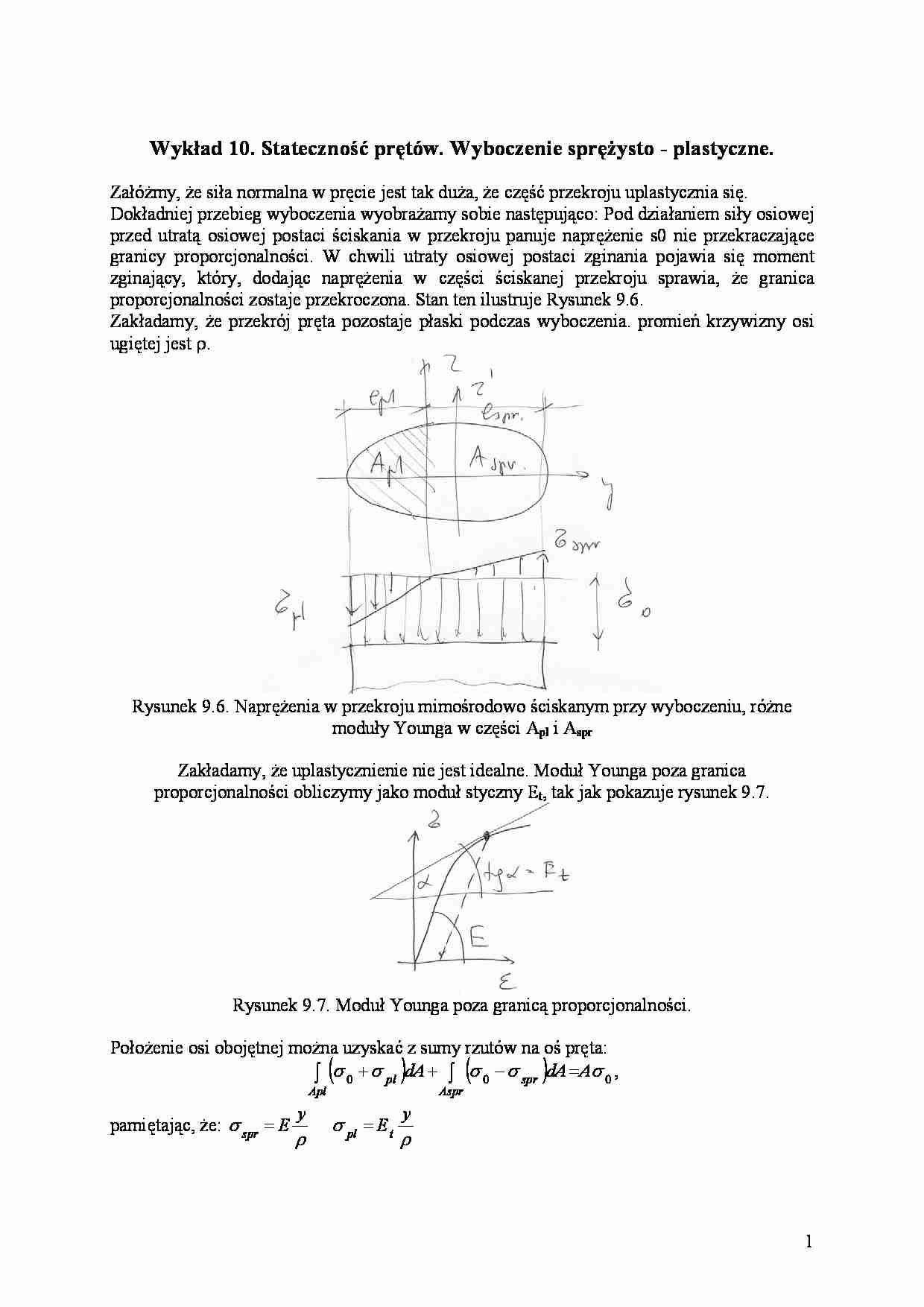
proporcjonalności zostaje przekroczona. Stan ten ilustruje Rysunek 9.6.
Zakładamy, że przekrój pręta pozostaje płaski podczas wyboczenia. promień krzywizny osi
ugiętej jest ρ.
Rysunek 9.6. Naprężenia w przekroju mimośrodowo ściskanym przy wyboczeniu, różne
moduły Younga w części Apl i Aspr
Zakładamy, że uplastycznienie nie jest idealne. Moduł Younga poza granica
proporcjonalności obliczymy jako moduł styczny Et, tak jak pokazuje rysunek 9.7.
Rysunek 9.7. Moduł Younga poza granicą proporcjonalności.
Położenie osi obojętnej można uzyskać z sumy rzutów na oś pręta:
∫ σ 0 + σ pl dA + ∫ σ 0 − σ spr dA =Aσ 0 ,
(
)
Apl
pamiętając, że: σ spr = E
y
ρ
(
)
Aspr
σ pl = E t
y
ρ
1
Z równania równowagi wynika, że oś obojętna dzieli przekrój tak, że momenty statyczne
części przekroju: Spl i Sspr spełniają zależność:
EtSpl = ESspr
Zależność krzywizna-moment uzyskać można po prostych przekształceniach sumy
momentów:
∫ σ 0 + σ pl ydA − ∫ σ 0 − σ spr ydA =M
(
)
(
Apl
)
Aspr
Z równania powyższego wynika, że momenty bezwładności odpowiednich części przekroju
spełniają zależność:
1
M
M
= − y ′′ =
= *
E t J pl + EJ spr JE
ρ
J
J
E* jest modułem wyboczenia, pewnym zastępczym modułem Younga, który może być użyty
w podstawowych równaniach różniczkowych osi ugiętej zamiast E:
E t J pl + EJ spr
J
= E*
Na przykład wzory na smukłość pręta i naprężenie krytyczne modyfikują się następująco:
λ dop = π
E*
σ dop
σ kr
π 2 E*
= 2
λ
Wykres zależności σ−λ można przedstawić następująco:
σ
σgr
zakres poza granicą
proporcjonalności, E*
hiperbola Eulera, zakres
sprężysty, E*=E
λ
Rysunek 9.8. Wykres zależności σ−λ. Prosta przedstawia przybliżenie Tetmajera-Jasińskiego
zaś parabola wykreślona linią przerywaną - przybliżenie Ostenfelda.
Opis związku smukłość- naprężenie poza granicą proporcjonalności można przybliżyć
wzorem liniowym Tetmajera-Jasińskiego
σkr = a - bλ
lub parabolą Ostenfelda:
σkr = A - Bλ2
Parametry a, b, A, B można znaleźć w tabelach. Są one ustalane dla podstawowych
materiałów na podstawie doświadczeń.
2
... zobacz całą notatkę




Komentarze użytkowników (0)