To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
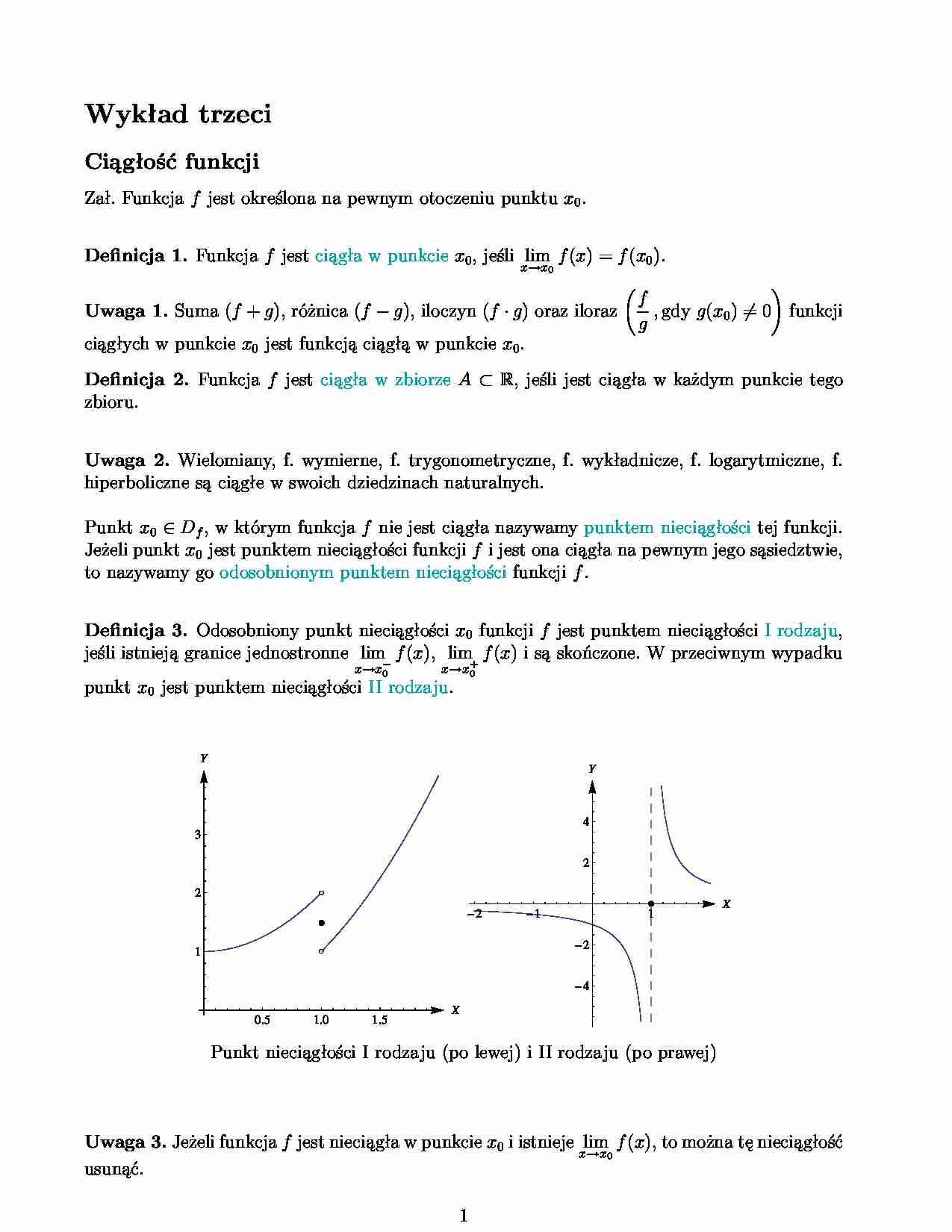


Wykład trzeci Ciągłość funkcji Zał. Funkcja f jest określona na pewnym otoczeniu punktu x 0. Definicja 1. Funkcja f jest ciągła w punkcie x 0, jeśli lim x→x 0 f ( x ) = f ( x 0). Uwaga 1. Suma ( f + g ), różnica ( f − g ), iloczyn ( f · g ) oraz iloraz f g , gdy g ( x 0) = 0 funkcji ciągłych w punkcie x 0 jest funkcją ciągłą w punkcie x 0. Definicja 2. Funkcja f jest ciągła w zbiorze A ⊂ R, jeśli jest ciągła w każdym punkcie tego zbioru. Uwaga 2. Wielomiany, f. wymierne, f. trygonometryczne, f. wykładnicze, f. logarytmiczne, f. hiperboliczne są ciągłe w swoich dziedzinach naturalnych. Punkt x 0 ∈ Df , w którym funkcja f nie jest ciągła nazywamy punktem nieciągłości tej funkcji. Jeżeli punkt x 0 jest punktem nieciągłości funkcji f i jest ona ciągła na pewnym jego sąsiedztwie, to nazywamy go odosobnionym punktem nieciągłości funkcji f . Definicja 3. Odosobniony punkt nieciągłości x 0 funkcji f jest punktem nieciągłości I rodzaju, jeśli istnieją granice jednostronne lim x→x − 0 f ( x ), lim x→x + 0 f ( x ) i są skończone. W przeciwnym wypadku punkt x 0 jest punktem nieciągłości II rodzaju. 0.5 1.0 1.5 X 1 2 3 Y 2 1 1 X 4 2 2 4 Y Punkt nieciągłości I rodzaju (po lewej) i II rodzaju (po prawej) Uwaga 3. Jeżeli funkcja f jest nieciągła w punkcie x 0 i istnieje lim x→x 0 f ( x ), to można tę nieciągłość usunąć. 1 Własności funkcji ciągłych 1. (tw. o ciągłości funkcji odwrotnej) Jeżeli funkcja f jest ciągła i rosnąca (odp.malejąca) na przedziale A ⊂ R, to f ( A ) jest przedziałem oraz funkcja odwrotna f − 1 jest ciągła i rosnąca (odp.malejąca) na przedziale f ( A ). 2. (tw. o lokalnym zachowaniu znaku) Jeżeli funkcja f jest ciągła w punkcie x 0 oraz f ( x 0) 0), to istnieje takie otoczenie O punktu x 0, że dla każdego x ∈ O ∩ Df zachodzi nierówność f ( x ) 0). Zastosowanie: jeżeli funkcja f jest ciągła w punkcie x 0 i f ( x 0) = 0, to na pewnym otoczeniu punktu x 0 wartości funkcji f mają ten sam znak co liczba f ( x 0). 3. (tw. o przyjmowaniu wartości pośrednich) Jeżeli funkcja f jest ciągła na przedziale A (domkniętym lub otwartym, ograniczonym lub nieograniczonym) oraz dla pewnych x 1 , x 2 ∈ A : f ( x 1) = a 1 = f ( x 2) = a 2, to dla każdej liczby c leżącej między a 1 i a 2 istnieje x ∈ A taki, że f ( x ) =
(…)
… na przedziale domkniętym a; b , to
(a) f jest ograniczona w a; b (tzn.∃m, M ∈ R ∀x ∈ a; b [m
f (x)
M ]),
(b) istnieją takie liczby x1 , x2 ∈ a; b , że sup f (x) = f (x1 ) oraz inf f (x) = f (x2 ).
x∈ a;b
x∈ a;b
Asymptoty pionowe
Zał. Funkcja f jest określona w pewnym sąsiedztwie (co najmniej jednostronnym) punktu x0 .
Definicja 4. Prosta x = x0 jest asymptotą pionową lewostronną (odp.prawostronną) krzywej
y = f…
... zobacz całą notatkę






Komentarze użytkowników (0)