To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
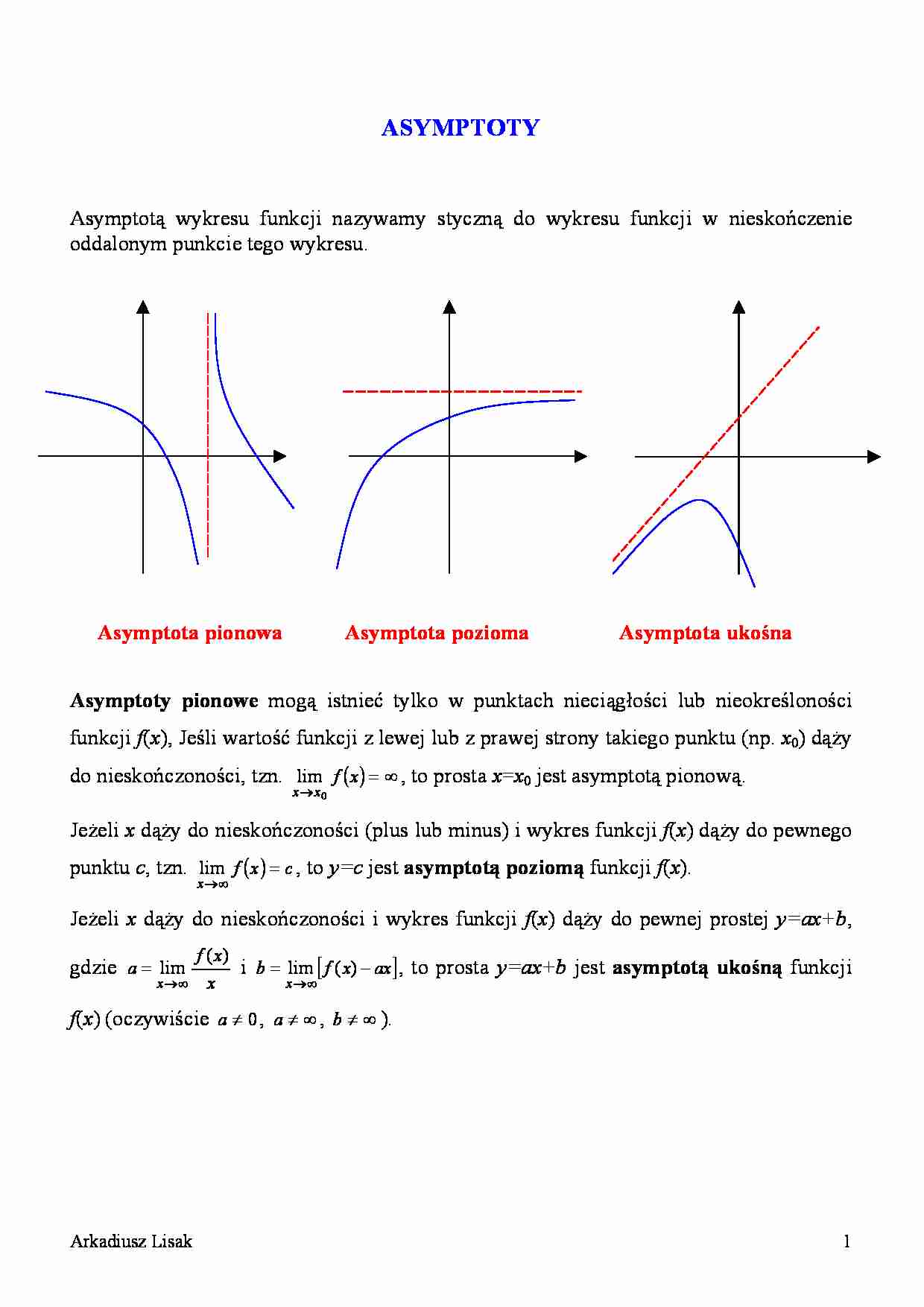

ASYMPTOTY Asymptotą wykresu funkcji nazywamy styczną do wykresu funkcji w nieskończenie oddalonym punkcie tego wykresu. Asymptota pionowa Asymptota pozioma Asymptota ukośna Asymptoty pionowe mogą istnieć tylko w punktach nieciągłości lub nieokreśloności funkcji f ( x ), Jeśli wartość funkcji z lewej lub z prawej strony takiego punktu (np. x 0) dąży do nieskończoności, tzn. , to prosta x = x ( ) ∞ = → x f x x 0 lim 0 jest asymptotą pionową. Jeżeli x dąży do nieskończoności (plus lub minus) i wykres funkcji f ( x ) dąży do pewnego punktu c , tzn. , to y=c jest asymptotą poziomą funkcji f ( x ). ( ) c x f x = ∞ → lim Jeżeli x dąży do nieskończoności i wykres funkcji f ( x ) dąży do pewnej prostej y=ax+b , gdzie x x f a x ) ( lim ∞ → = i , to prosta y=ax+b jest asymptotą ukośną funkcji f ( x ) (oczywiście a , a , b ). [ ax x f b x − = ∞ → ) ( lim 0 ∞ ≠ ∞ ≠ ] ≠ Arkadiusz Lisak 1 Przykład. 1. 1 1 + = x y , x . 1 − ≠ 0 1 1 lim = + −∞ → x x , 0 1 1 lim = + +∞ → x x , −∞ = + − − → 1 1 lim 1 x x , +∞ = + + − → 1 1 lim 1 x x Asymptota pozioma: y =0 Asymptota pionowa: x =-1 2. 2 2 3 1 5 3 x x x y + − = , 0 ≠ x 3 1 5 3 lim 3 2 3 = + − = ∞ → x x x a x , 5 1 5 lim 3 1 5 3 lim 3 1 5 3 lim 2 2 2 3 2 3 2 2 3 − = + − = − + − = − + − = ∞ → ∞ → ∞ → x x x x x x x x x x x x x b Asymptota ukośna: y=3x-5 . OBLICZANIE POCHODNEJ Z DEFINICJI x x f x x f x f x ∆ − ∆ + = → ∆ ) ( ) ( lim ) ( ' 0 Przykład. 2 ) ( x x f = = ∆ − ∆ + ∆ + = ∆ − ∆ + = ∆ − ∆ + = → ∆ → ∆ → ∆ x x x x x x x x x x x x f x x f x f x x x 2 2 2 0 2 2 0 0 2 lim ) ( lim ) ( ) ( lim ) ( ' ( ) x x x x x x x x x x x x x x 2 2 lim ) 2 ( lim 2 lim 0 0 2 0 = ∆ + = ∆ ∆ ∆ + = ∆ ∆ + ∆ = → ∆
... zobacz całą notatkę




Komentarze użytkowników (0)