To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Przykład 9.3. Wyboczenie układu belka-słup
Wyznaczyć wartość krytyczną siły
P obciążającej głowicę słupa. Słup
jest częścią układu ramowego,
którego drugim elementem jest
belka pozioma. Węzeł słup-belka
jest sztywny. Oznacza to, że obrót
przekroju
belki
położonego
nieskończenie blisko węzła jest
równy obrotowi przekroju słupa
sąsiadującego z tym węzłem.
Fundament pod węzłem jest
niepodatny, podpora B belki jest
niepodatna, przesuwna. Przyjąć
wysokość słupa H, długość belki L.
Moduły bezwładności przekrojów
słupa i belki wynoszą odpowiednio
Js i Jb zaś moduły Younga
materiałów - Es i Eb. W
płaszczyźnie
prostopadłej
do
rysunku słup i belka są usztywnione
ścianą i stropem.
P
C
Es, Js
H
Eb, Jb
A
B
L
Rysunek 1. Schematy statyczne układu belkasłup.
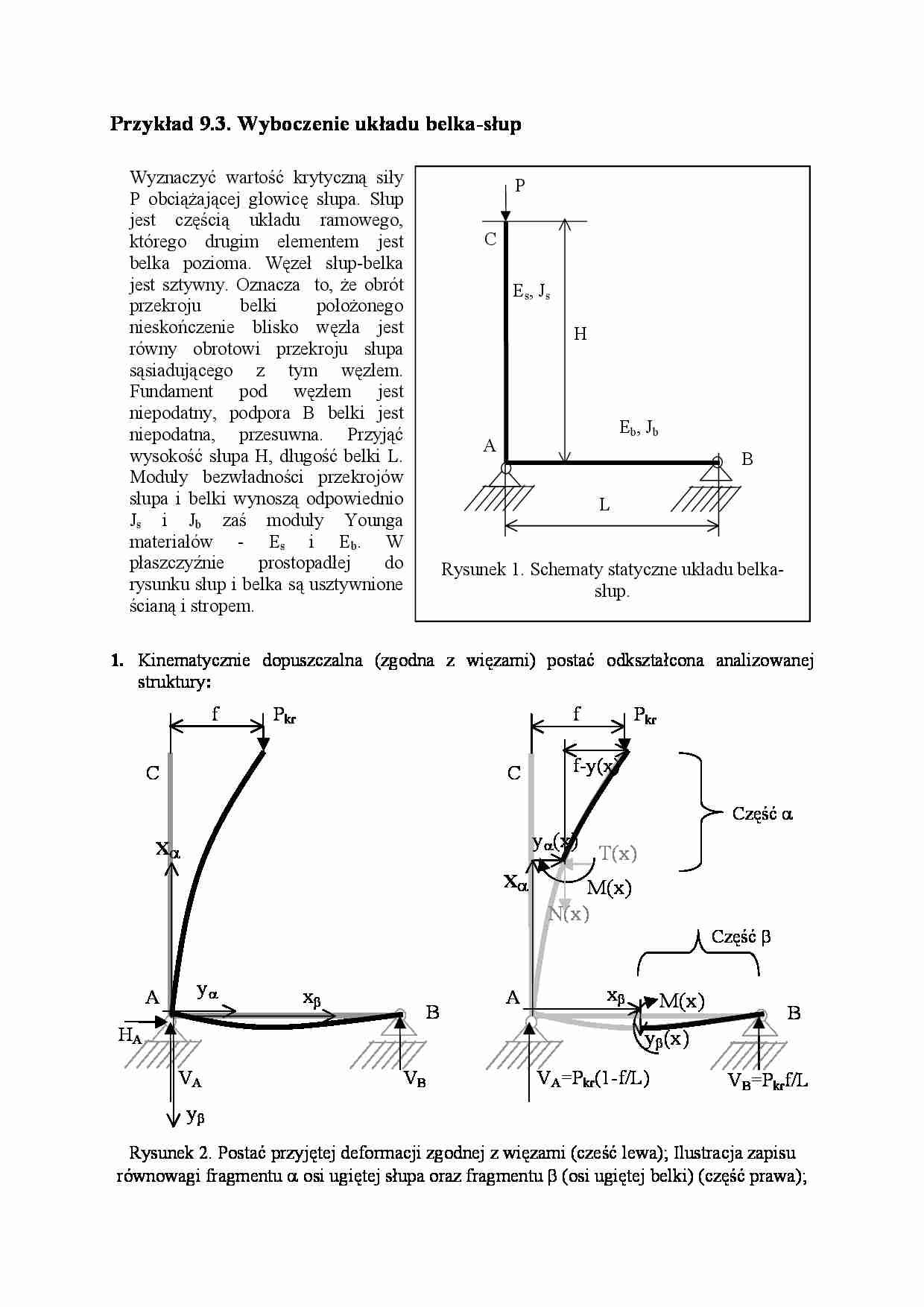
1. Kinematycznie dopuszczalna (zgodna z więzami) postać odkształcona analizowanej
struktury:
f
Pkr
f
C
C
Pkr
f-y(x)
Część α
yα(x)
xα
A
xα
yα
HA
VA
xβ
B
VB
A
T(x)
M(x)
N(x)
Część β
xβ
M(x)
yβ(x)
VA=Pkr(1-f/L)
B
VB=Pkrf/L
yβ
Rysunek 2. Postać przyjętej deformacji zgodnej z więzami (cześć lewa); Ilustracja zapisu
równowagi fragmentu α osi ugiętej słupa oraz fragmentu β (osi ugiętej belki) (część prawa);
2. Równania równowagi dla dowolnego, odkształconego fragmentu struktury:
Reakcje obliczymy biorąc pod uwagę sumę momentów względem punktu A dla odkształconej
ramy wyobrażonej na Rys. 2:
VBL=Pkrf
=
VB=Pkrf/L
Reakcja w podporze A nie będzie potrzebna w dalszych obliczeniach. Z sumy rzutów na oś
poziomą zauważamy, że jej składowa pozioma jest równa zeru zaś z sumy rzutów sił na oś
pionową wynika wartość VA podana na Rys. 2.
Wobec tego, że w ramie wyróżnia się dwa jakościowo różne fragmenty, w których równania
momentów zginających jako funkcji x są różne, należy rozpatrzyć dwa przypadki w zapisie
warunków równowagi. Pierwszy z tych fragmentów to słup, drugi to belka. Zauważmy, że
siła osiowa występuje tylko w słupie. Belka poddana jest tylko zginaniu, zależnemu jednak od
siły krytycznej.
2.a.
Dla części α (słup):
M ( x) + Pkr ( f − yα ( x)) = 0 = M ( x) = Pkr ( yα ( x) − f )
′
ponieważ: M ( x) = − yα′ ( x)Es J s otrzymuje się równanie różniczkowe dla osi ugiętej:
′
′
= yα′ ( x)Es J s = Pkr ( f − yα ( x)) = yα′ ( x)Es J s + Pkr yα ( x) = Pkr f =
′
yα′ ( x) + k 2 yα ( x) = k 2 f
oznaczono tu (jak zwykle w zagadnieniach wyboczenia)
k2 =
(1)
Pkr
Es J s
(2)
Rozwiązanie równania (1) jest postaci:
yα ( x) = A cos(kx)+ B sin(kx)+ yszcz (x)
ponieważ yszcz (x )= f wiec ostatecznie:
yα ( x) = A cos(kx)+ B sin(kx)+ f
2.b.
(3)
Dla części β (belka):
Moment zapisać można (dla części prawej belki – patrz rysunek 2.) następująco:
M ( x) = Pkr
= Eb J b y′′ ( x) = −Pkr
β
f
(L − x)
L
f
(L − x) = y′β′ ( x) = Pkr f x − Pkr f
L
Eb J b L
Eb J b
(4)
=
Otrzymane równanie różniczkowe zawiera tylko druga pochodną linii ugięcia wobec tego
rozwiązuje się je przez bezpośrednie całkowanie:
yβ ( x) =
2
Pkr f x3 Pkr
−
f x + Cx + D
Eb J b L 6 Eb J b 2
(5)
Zauważmy, że całkowanie równania (4)
(…)
…
Es J s L
= ctg kH
3Eb J b
(12)
z
Es J s L
= ctg ( z)
3Eb J b H
(13)
podstawiając: kH=z otrzymujemy:
3
Rozwiązanie można odczytać z wykresu pokazanego na rysunku (punkt przecięcia prostej i
cotangensoidy):
tgγ =
γ
Es J s L
3Eb J b H
Π/2
z
z0
Rysunek 3. Graficzny sposób wyznaczenia miejsca zerowego wyznacznika głównego układu
równań (10). Rysunek ten pozwala również zrozumieć jak zmienia…
... zobacz całą notatkę






Komentarze użytkowników (0)