To tylko jedna z 6 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
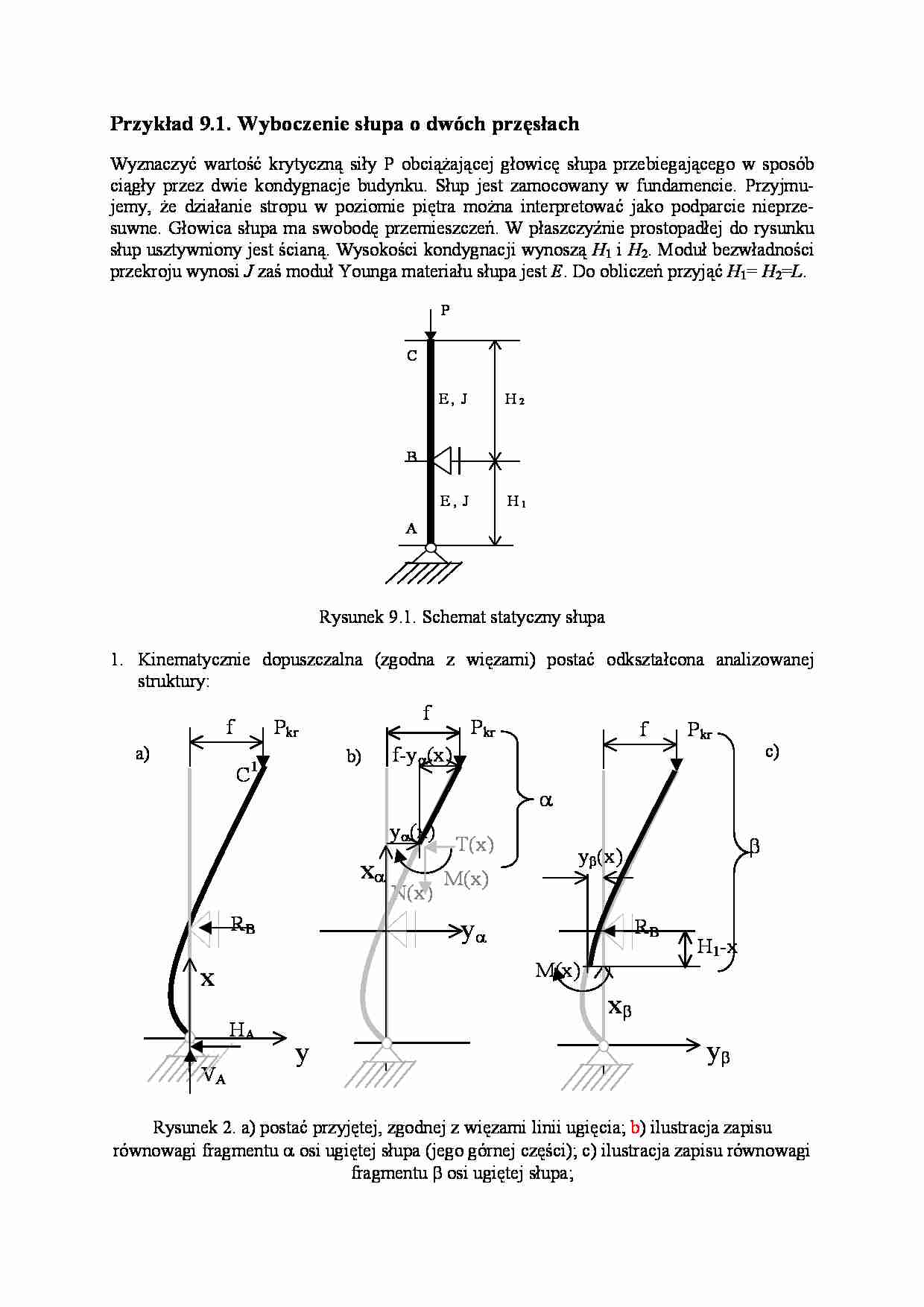


Przykład 9.1. Wyboczenie słupa o dwóch przęsłach
Wyznaczyć wartość krytyczną siły P obciążającej głowicę słupa przebiegającego w sposób
ciągły przez dwie kondygnacje budynku. Słup jest zamocowany w fundamencie. Przyjmujemy, że działanie stropu w poziomie piętra można interpretować jako podparcie nieprzesuwne. Głowica słupa ma swobodę przemieszczeń. W płaszczyźnie prostopadłej do rysunku
słup usztywniony jest ścianą. Wysokości kondygnacji wynoszą H1 i H2. Moduł bezwładności
przekroju wynosi J zaś moduł Younga materiału słupa jest E. Do obliczeń przyjąć H1= H2=L.
P
C
E, J
H2
E, J
H1
B
A
Rysunek 9.1. Schemat statyczny słupa
1. Kinematycznie dopuszczalna (zgodna z więzami) postać odkształcona analizowanej
struktury:
f
a)
f
Pkr
b)
1
C
f
f-yα(x)
xα
RB
N(x)
T(x)
c)
M(x)
β
yβ(x)
yα
RB
M(x)
x
HA
Pkr
α
yα(x)
VA
Pkr
H1-x
xβ
y
yβ
Rysunek 2. a) postać przyjętej, zgodnej z więzami linii ugięcia; b) ilustracja zapisu
równowagi fragmentu α osi ugiętej słupa (jego górnej części); c) ilustracja zapisu równowagi
fragmentu β osi ugiętej słupa;
2. Równania równowagi dowolnego odkształconego fragmentu struktury
Wobec tego, że w słupie wyróżnia się dwa przedziały w których równania momentów
zginających są różnymi funkcjami zmiennej niezależnej x, należy rozpatrzyć te dwa
przypadki w zapisie warunków równowagi odkształconego fragmentu struktury. Podział na
przedziały pokazany jest na rysunku 2.
Zauważmy, że układ współrzędnych dla części α (xα yα) ma początek w punkcie B (podpora)
zaś układ współrzędnych dla części β (xβ yβ) ma początek w punkcie A (podstawa słupa).
Zadanie jest statycznie wyznaczalne wobec tego łatwo jest obliczyć reakcje:
Suma momentów względem punktu A daje:
Suma rzutów sił na oś poziomą daje:
Suma rzutów sił na oś pionową daje:
RBH1=Pkrf = RB=Pkrf/ H1
HA=-Pkrf/ H1
VA=Pkr
Dla części α piszemy sumę momentów względem punktu o współrzędnej xα (w ten sposób w
równaniu nie pojawią się siły tnąca i normalna w tym punkcie):
M ( x) + Pkr ( f − yα ( x))= 0 = M ( x) = Pkr ( yα ( x) − f ) =
′
ponieważ: M ( x) = − yα′ ( x) EJ wobec tego:
′
′
yα′ ( x)EJ = Pkr ( f − yα ( x)) = yα′ ( x)EJ + Pkr yα ( x) = Pkr f
po uporządkowaniu otrzymujemy równanie różniczkowe zwyczajne drugiego rzędu:
′
yα′ ( x) + k 2 yα ( x) = k 2 f
(1)
oznaczono tu (jak zawsze w zagadnieniach wyboczenia)
P
k 2 = kr
(2)
EJ
Rozwiązaniem tego równania ma następującą postać (jak wiadomo z podstawowego kursu
matematyki i co łatwo sprawdzić przez podstawienie (3) do (1)):
yα ( x) = A cos(kx)+ B sin(kx)+ yszcz (x) .
Ponieważ yszcz (x )= f wiec ostatecznie:
yα ( x) = A cos(kx)+ B sin(kx)+ f
(3)
Zasady ustalania yszcz(x) dla równania różniczkowego niejednorodnego należy przypomnieć
sobie z kursu podstawowego matematyki. W zagadnieniach związanych z wyboczeniem
wyraz wolny w równaniu różniczkowym jest najczęściej wielomianem. Wobec tego
rozwiązanie szczególne też ma postać wielomianu o nieznanych współczynnikach.
Współczynniki te łatwo jest ustalić porównując
(…)
… rozwiązania nietrywialnego jest zerowanie się wyznacznika macierzy
wyrazów przy niewiadomych (należy przypomnieć sobie z kursu matematyki odpowiednie
twierdzenie o istnieniu rozwiązania układu równań liniowych). Otrzymujemy z tego warunku
następujące równanie przestępne:
W = −kH1 sin(kH1 )cos(kH 2 )+ sin(kH 2 )sin(kH1 )− kH1 sin(kH 2 )cos(kH1 ) = 0
(12)
Określmy zmienną bezwymiarową t:
t = kH1
(13)
(t jest tu zmienną pomocniczą, nie ma ona, oczywiście, nic wspólnego z czasem, tradycyjnie
oznaczanym tym symbolem):
H
H
H
t sin(t )cos 2 t − sin 2 t sin(t )+ t sin 2 t cos(t ) = 0
(14)
H
H
H
1
1
1
3
Ponieważ wyznacznik W zależy za pośrednictwem t od Pkr:
P
t = H1 kr
(15)
EJ
można znaleźć taką siłę Pkr, przy której wyznacznik ma swoje miejsce zerowe.
Dalsze obliczenia wykonano…
... zobacz całą notatkę






Komentarze użytkowników (0)