To tylko jedna z 6 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
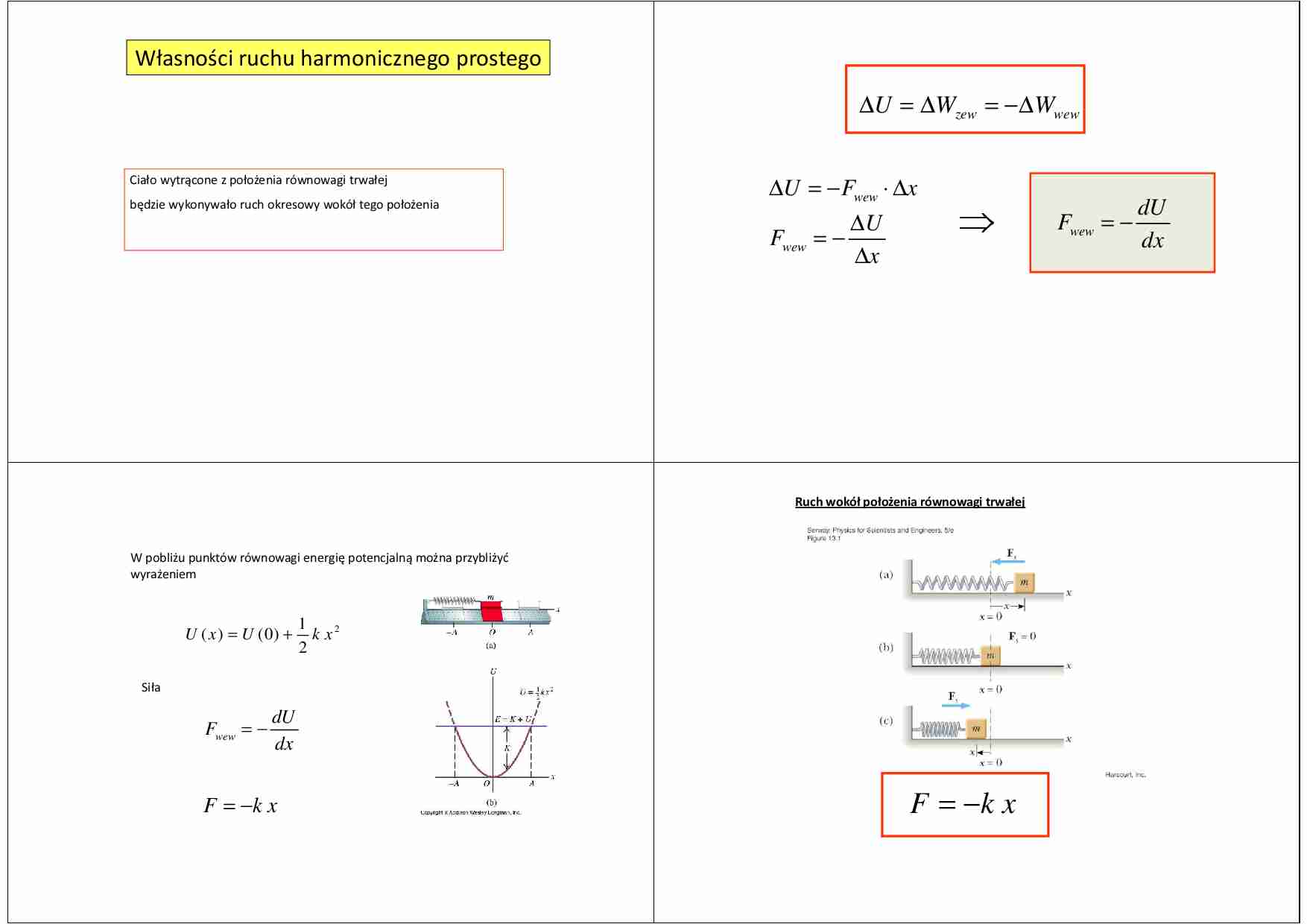


Własności ruchu harmonicznego prostego
∆U = ∆Wzew = −∆Wwew
Ciało wytrącone z położenia równowagi trwałej
będzie wykonywało ruch okresowy wokół tego położenia
∆U = − Fwew ⋅ ∆x
Fwew
∆U
=−
∆x
⇒
Ruch wokół położenia równowagi trwałej
W pobliżu punktów równowagi energię potencjalną można przybliżyć
wyrażeniem
U ( x ) = U (0) +
1
k x2
2
Siła
Fwew = −
dU
dx
F = −k x
F = −k x
Fwew = −
dU
dx
Własności ruchu harmonicznego prostego
Ruch harmoniczny prosty
Położenie cząstki w dowolnej chwili t:
• W dowolnej chwili
F = ma
a
•
F = -kx
Ale tutaj F = -kx
k
•
a
m
Więc:
A…amplituda
ma = m
d x
= − kx
dt 2
d x
k
=− x
m
dt 2
niech
x
2
2
k
ω=
m
ω…częstość
φ…faza początkowa
T…okres
(ωt + Φ)…faza
równanie różniczkowe na x(t)
d 2x
+ ω2x = 0
2
dt
Własności ruchu harmonicznego prostego
φ=0
•
x(t ) = A cos(ωt + φ )
ω=
F = − kx
2π
k
=
T
m
∆U = −Ws =
Jeżeli ruch odbywa się wokół położenia
równowagi x=0, można przyjąć:
Położenie
x(t ) = A cos(ωt + φ )
•
Prędkość
v(t ) = −ω A sin(ωt + φ )
•
1
2
k ( x2 − x12 )
2
Przyspieszenie
a (t ) = −ω 2 A cos(ωt + φ )
U (0) = 0
wówczas
U ( x) =
1 2
kx
2
Ec = U + Ek
Własności ruchu harmonicznego prostego
Energia całkowita oscylatora harmonicznego
1
1
E = Ek + U = 2 mv 2 + 2 kx 2
x ( t ) = A cos (ω t + φ )
v ( t ) = −ω A sin (ω t + φ )
1
1
E = 2 m −ω A sin (ω t + φ ) + 2 k A cos (ω t + φ )
2
2
2
2
1
E = 2 A mω sin (ω t + φ ) + k cos (ω t + φ )
2
Ek =
1
2
m (ω A sin( ω t + φ ) )
2
Ale
ω2 = k m
skąd
1
1
E = 2 kA2 sin2 (ω t + φ ) + cos2 (ω t + φ ) = 2 kA2
1
E p = kx 2
2
1
1
E = 2 kA2 = 2 ω 2 mA2
Wahadło matematyczne
Wahadło fizyczne
F = − mg sin θ
sin θ ≈ θ
F = −mg sin θ ≈ − mgθ
dla małych kątów :
F =−
mg
g
Lθ = − m s = − ks
L
L
ω=
k
mg / L
=
=
m
m
T=
2π
ω
= 2π
L
g
g
L
T = 2π
I
mgh
2
Wahadło torsyjne
Ruch harmoniczny tłumiony
Siła oporu
Fo = −b v
M = −kθ
b - stała tłumienia
Fwyp = − kx − bv
T = 2π
ma = − kx − bv
I
k
m
gdzie I jest momentem
bezwładności układu
d 2x
dx
+ b + kx = 0.
2
dt
dt
Wprowadźmy nowe oznaczenie
β=
b
k
; ω0 =
2m
m
d 2x
dx
+ 2β
+ ω0 x = 0.
2
dt
dt
Rozwiązanie - zależność położenia od czasu
β ≤ ω0
Wówczas w przypadku małych tłumień gdy
x(t ) = A0 e − β t cos(ωt + φ )
)
(
2
x (t ) = Ae− βt cos ω0 − β 2 t + φ =A(t) cos(ω t+φ )
Energia drgań w przypadku małych tłumień
gdzie:
ω = ω02 − β 2
oraz
A(t ) = A0e − β t
E (t ) ≈
1
1
2
k ( A ( t ) ) = kA02 e − 2 β t = E 0 e − 2 β t
2
2
Jak wyznaczyć współczynnik tłumienia β ?
Ruch harmoniczny tłumiony
relaksacja
A(t ) = A0e − β t
A(t + T ) = A0e
2
(a) ω 0 = β 2
− β ( t +T )
= A0e
−βt
A0e
A(t )
ln
= ln A e − β t e − β T
A(t + T )
0
− β t − βT
= βT
e
x ( t ) = A0e − β t cos
(
2
ω0 − β 2 t + φ
)
⇒ x = A0e − β t cos φ
układ wraca ekspotencjalnie to położenia równowagi.
2
(b) ω 0
... zobacz całą notatkę






Komentarze użytkowników (0)