To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
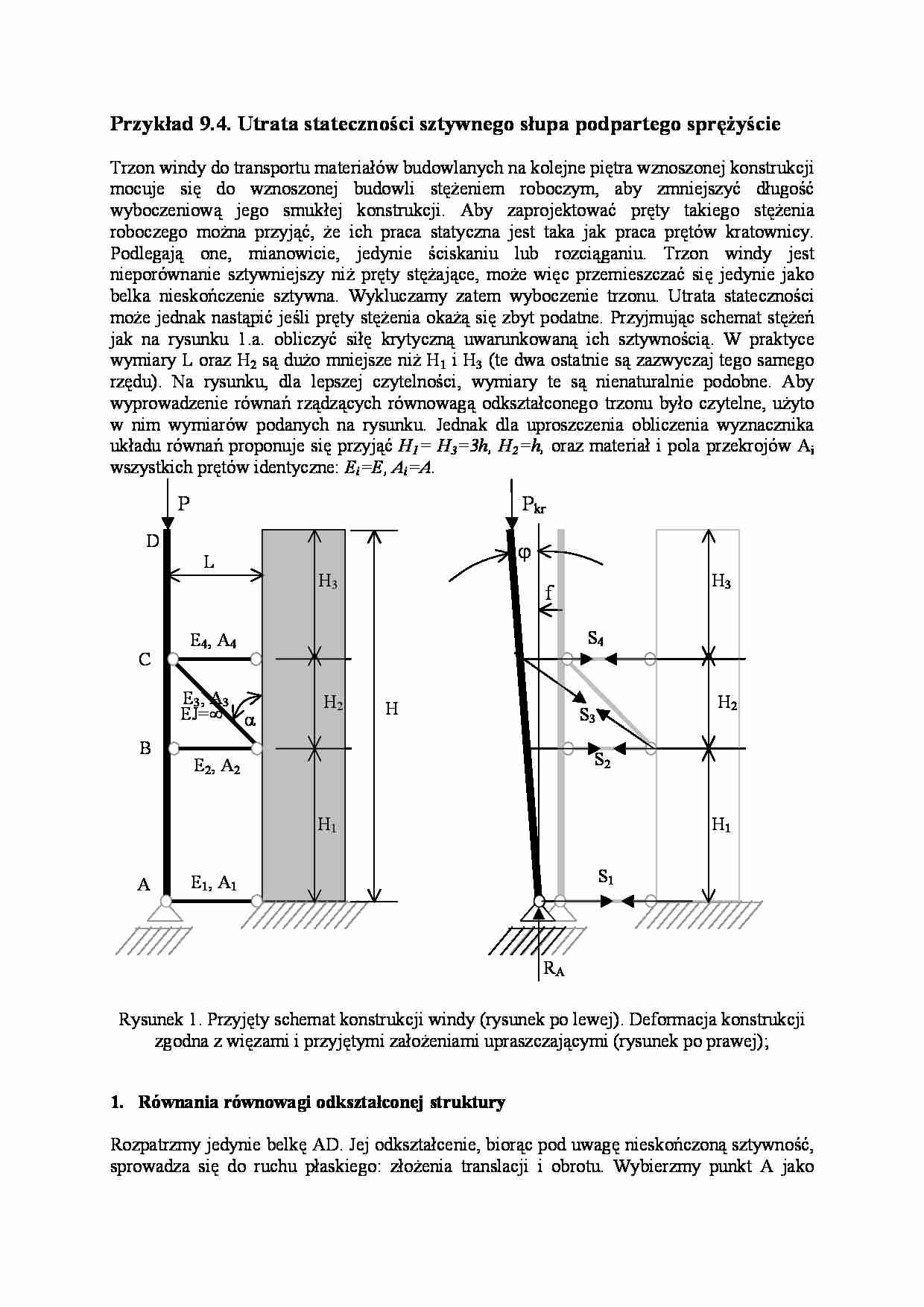


Przykład 9.4. Utrata stateczności sztywnego słupa podpartego sprężyście
Trzon windy do transportu materiałów budowlanych na kolejne piętra wznoszonej konstrukcji
mocuje się do wznoszonej budowli stężeniem roboczym, aby zmniejszyć długość
wyboczeniową jego smukłej konstrukcji. Aby zaprojektować pręty takiego stężenia
roboczego można przyjąć, że ich praca statyczna jest taka jak praca prętów kratownicy.
Podlegają one, mianowicie, jedynie ściskaniu lub rozciąganiu. Trzon windy jest
nieporównanie sztywniejszy niż pręty stężające, może więc przemieszczać się jedynie jako
belka nieskończenie sztywna. Wykluczamy zatem wyboczenie trzonu. Utrata stateczności
może jednak nastąpić jeśli pręty stężenia okażą się zbyt podatne. Przyjmując schemat stężeń
jak na rysunku 1.a. obliczyć siłę krytyczną uwarunkowaną ich sztywnością. W praktyce
wymiary L oraz H2 są dużo mniejsze niż H1 i H3 (te dwa ostatnie są zazwyczaj tego samego
rzędu). Na rysunku, dla lepszej czytelności, wymiary te są nienaturalnie podobne. Aby
wyprowadzenie równań rządzących równowagą odkształconego trzonu było czytelne, użyto
w nim wymiarów podanych na rysunku. Jednak dla uproszczenia obliczenia wyznacznika
układu równań proponuje się przyjąć H1= H3=3h, H2=h, oraz materiał i pola przekrojów Ai
wszystkich prętów identyczne: Ei=E, Ai=A.
P
Pkr
D
L
C
H3
H3
f
S4
E4, A4
E3, A3
EJ=∞ α
B
ϕ
H2
H
H2
S3
S2
E2, A2
H1
A
H1
S1
E1, A1
RA
Rysunek 1. Przyjęty schemat konstrukcji windy (rysunek po lewej). Deformacja konstrukcji
zgodna z więzami i przyjętymi założeniami upraszczającymi (rysunek po prawej);
1. Równania równowagi odkształconej struktury
Rozpatrzmy jedynie belkę AD. Jej odkształcenie, biorąc pod uwagę nieskończoną sztywność,
sprowadza się do ruchu płaskiego: złożenia translacji i obrotu. Wybierzmy punkt A jako
biegun i przedstawmy ruch belki jako ruch bieguna (przemieszczenie poziome o wektor f)
oraz obrót wokół bieguna o kąt ϕ. Przyjmijmy, że zarówno f jak i kąt ϕ są małe:
sin ϕ
≅1
cosϕ ≅ 1
ϕ
Oznaczono (rys. 1.a.):
H1+H2+H3=H;
α=arctg(L/H)
Napiszemy sumę momentów względem punktu A oraz sumę rzutów na oś poziomą
wszystkich sił działających na belkę wyobrażoną na Rys. 1.b.
Zapisanie trzeciego równania (sumy rzutów sił na oś pionową) wprowadza dodatkowo do
procedury rozwiązania - reakcję w podporze niepodatnej.
(1)
∑ M A =0 = H1S2 + (H1 + H 2 )(S3 sinα + S4 )− ( f +ϕH )Pkr = 0
S1 + S2 + S3 sinα + S4 = 0
(2)
∑ Fx =0 =
Należy teraz skorzystać z warunków geometrycznych oraz prawa fizycznego wiążącego
odkształcenia prętów z siłami, które w nich występują.
Wydłużenia prętów δ zgodne z założonym ruchem sztywnym belki są następujące
(rozciąganie ze znakiem „+”):
δ1 = f δ 2 = f +ϕH1
δ 3 = ( f +ϕ (H1 + H 2 ))sinα
δ 4 = f +ϕ (H1 + H 2 )
(3)
We wzorze (33) przemieszczenie poziome rzutowano na kierunek pręta, uzyskując w ten
sposób przybliżoną wartość zmiany jego długości. Ścisłe uzasadnienie prawidłowości takiego
przybliżenia przekracza ramy tego zadania i powinno być znane z kursu
... zobacz całą notatkę






Komentarze użytkowników (0)