To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
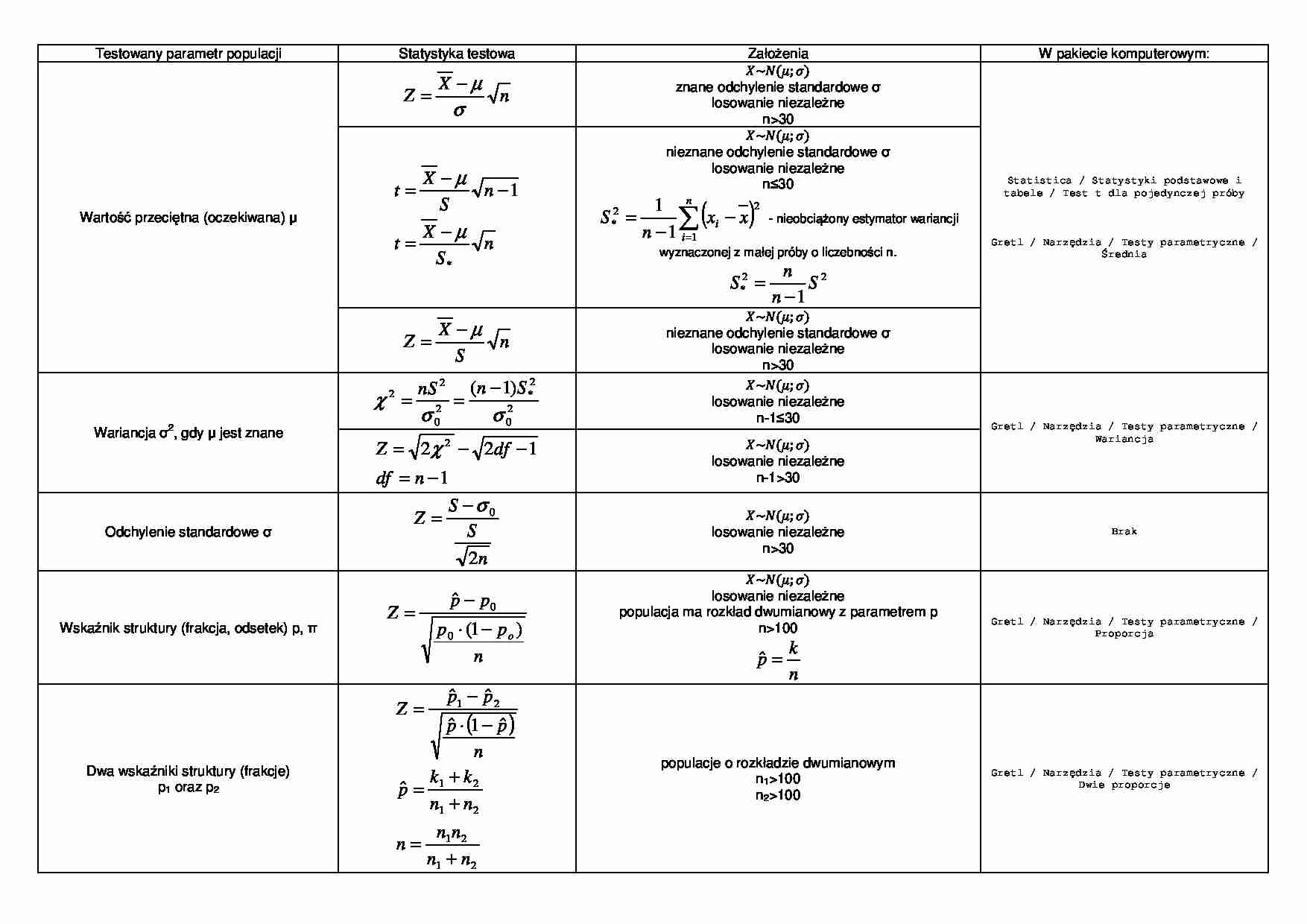
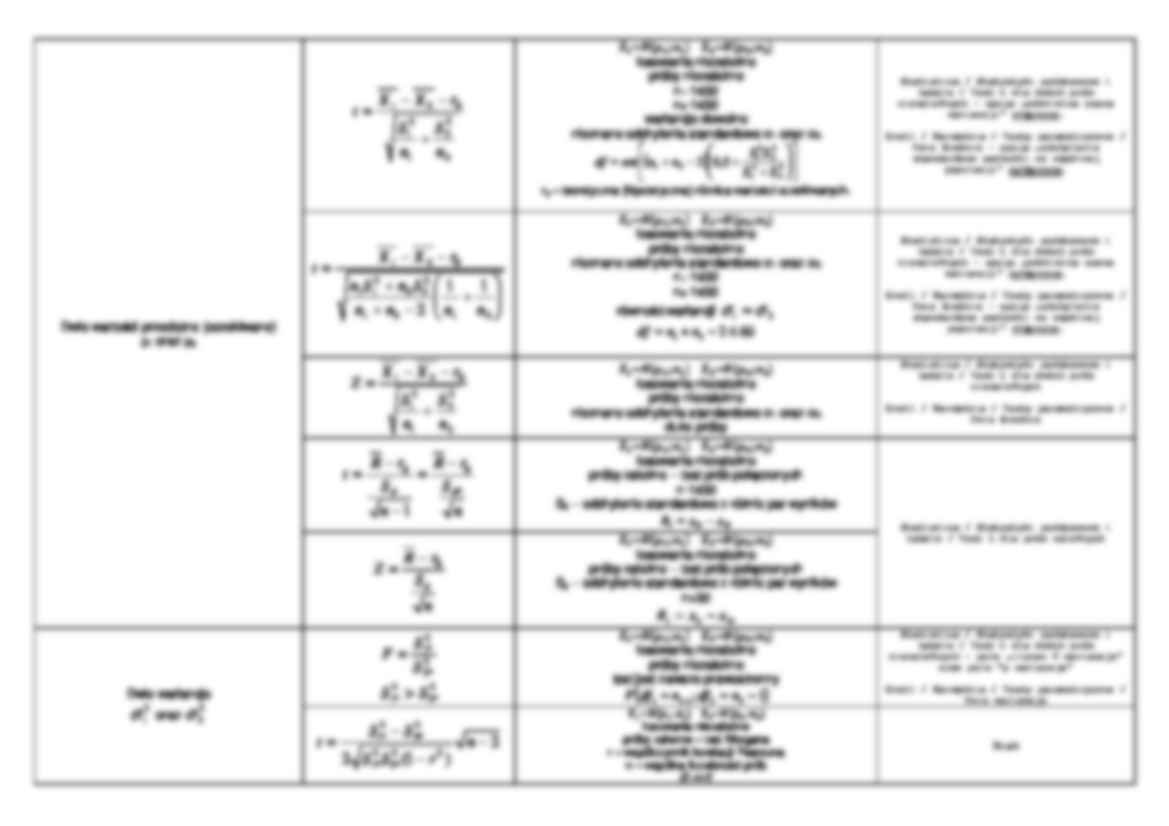
Testowany parametr populacji Statystyka testowa Zało żenia W pakiecie komputerowym: Warto ść przeciętna (oczekiwana) µ n X Z σ µ − = ܺ~ܰ(ߤ; ߪ) znane odchylenie standardowe σ losowanie niezale żne n30 Statistica / Statystyki podstawowe i tabele / Test t dla pojedynczej próby Gretl / Narz ędzia / Testy parametryczne / Średnia n S X t n S X t * 1 µ µ − = − − = ܺ~ܰ(ߤ; ߪ) nieznane odchylenie standardowe σ losowanie niezale żne n ≤30 ( ) ∑ = − − = n i i x x n S 1 2 2 * 1 1 - nieobciążony estymator wariancji wyznaczonej z małej próby o liczebności n. 2 2 * 1 S n n S − = n S X Z µ − = ܺ~ܰ(ߤ; ߪ) nieznane odchylenie standardowe σ losowanie niezale żne n30 Wariancja σ 2, gdy µ jest znane 2 0 2 * 2 0 2 2 ) 1 ( σ σ χ S n nS − = = ܺ~ܰ(ߤ; ߪ) losowanie niezale żne n-1 ≤30 Gretl / Narz ędzia / Testy parametryczne / Wariancja 1 1 2 2 2 − = − − = n df df Z χ ܺ~ܰ(ߤ; ߪ) losowanie niezale żne n-130 Odchylenie standardowe σ n S S Z 2 0 σ − = ܺ~ܰ(ߤ; ߪ) losowanie niezale żne n30 Brak Wska źnik struktury (frakcja, odsetek) p, π n p p p p Z o ) 1 ( ˆ 0 0 − ⋅ − = ܺ~ܰ(ߤ; ߪ) losowanie niezale żne populacja ma rozkład dwumianowy z parametrem p n100 n k p = ˆ Gretl / Narz ędzia / Testy parametryczne / Proporcja Dwa wska źniki struktury (frakcje) p1 oraz p2 ( ) 2 1 2 1 2 1 2 1 2 1 ˆ ˆ 1 ˆ ˆ ˆ n n n n n n n k k p n p p p p Z + = + + = − ⋅ − = populacje o rozkładzie dwumianowym n1100 n2100 Gretl / Narz ędzia / Testy parametryczne / Dwie proporcje Dwie warto ści przeciętne (oczekiwane) µ1 oraz µ2 2 2 2 1 2 1 0 2 1 n S n S r X X t + − − = ܺଵ~ܰሺߤଵ; ߪଵሻ ܺଶ~ܰ(ߤଶ; ߪଶ) losowania niezale żne próby niezale żne n1-1≤30 n2-1≤30 wariancje dowolne nieznane odchylenia standardowe σ1 oraz σ2 ( ) + + − + = 4 2 4 1 2 2 2 1 2 1 5 , 0 2 S S S S n n ent df r0 – teoretyczna (hipotetyczna) różnica wartości oczekiwanych.
... zobacz całą notatkę




Komentarze użytkowników (0)