To tylko jedna z 11 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Wiele zadań obliczeniowych ze statystyki wraz z rozwiązaniami. Liczebność skumulowana. Rodzaj szeregu statystycznego. Pozycyjne miary tendencji centralnej. Miary klasyczne, miary pozycyjne, miary nieabsolutne. Miary uzupełniające - typowe obszary zmienności. Środek przedziału. Rozkład jednomodalny. Mediana. Średnia arytmetyczna, dominanta. Zbiorowość statystyczna, jednostka i cecha. Histogram zwykły. Diagram skumulowany. Kwartyl. Wyznaczanie dominanty metodą graficzną. Odchylenie standardowe, pozycyjny współczynnik zmienności. Miary asymetrii.Analiza porównawcza.
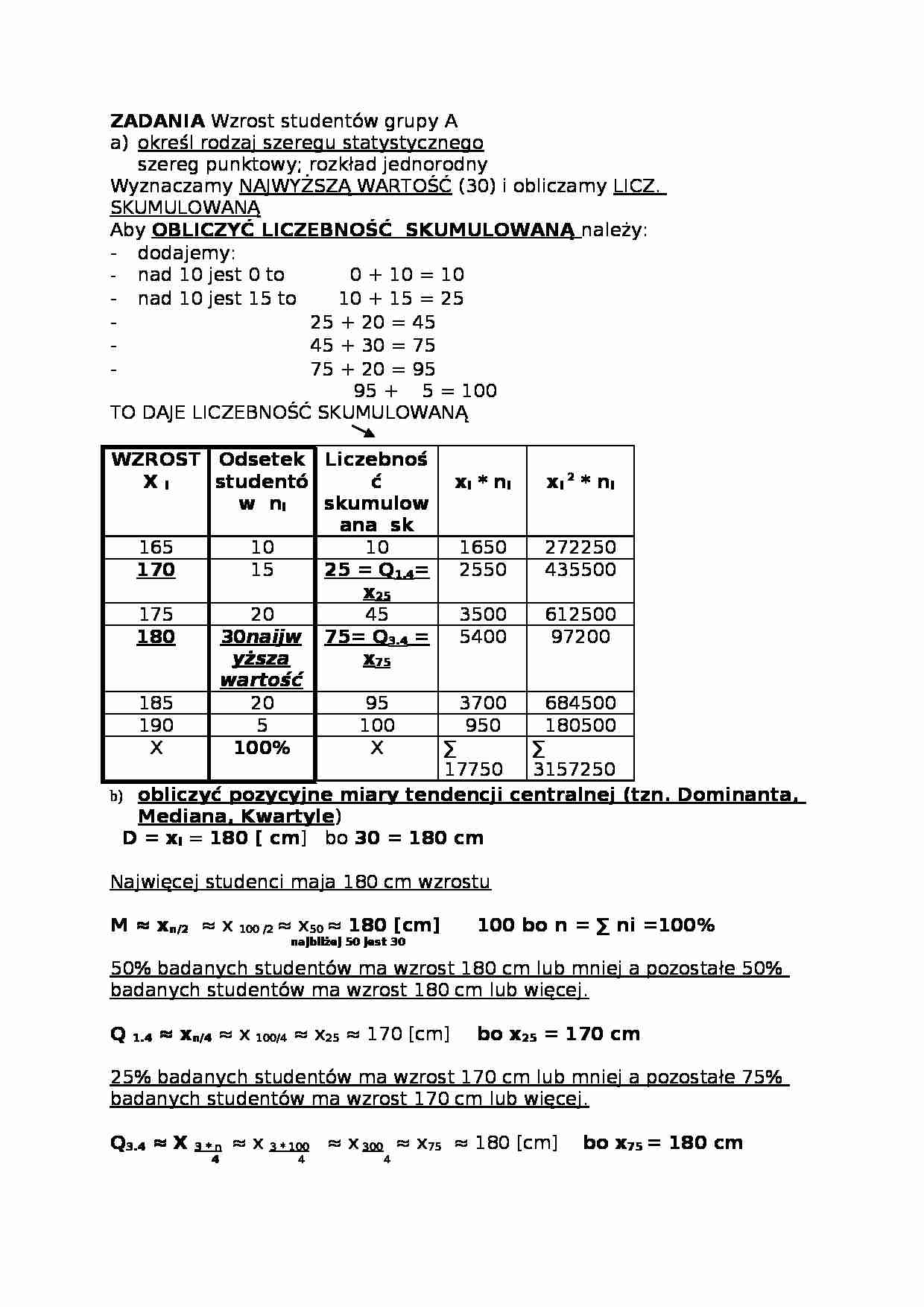
ZADANIA Wzrost studentów grupy A
określ rodzaj szeregu statystycznego
szereg punktowy; rozkład jednorodny
Wyznaczamy NAJWYŻSZĄ WARTOŚĆ (30) i obliczamy LICZ. SKUMULOWANĄ
Aby OBLICZYĆ LICZEBNOŚĆ SKUMULOWANĄ należy:
dodajemy: nad 10 jest 0 to 0 + 10 = 10
nad 10 jest 15 to 10 + 15 = 25
25 + 20 = 45
45 + 30 = 75
75 + 20 = 95
95 + 5 = 100
TO DAJE LICZEBNOŚĆ SKUMULOWANĄ
WZROST
X i
Odsetek studentów ni
Liczebność skumulowana sk
xi * ni
xi 2 * ni
165
10
10
1650
272250
170
15
25 = Q1.4= x25
2550
435500
175
20
45
3500
612500
180
30naijwyższa wartość
75= Q3.4 = x75
5400
97200
185
20
95
3700
684500
190
5
100
950
180500
X
100%
X
∑ 17750
∑ 3157250
obliczyć pozycyjne miary tendencji centralnej (tzn. Dominanta, Mediana, Kwartyle)
D = xi = 180 [ cm] bo 30 = 180 cm
Najwięcej studenci maja 180 cm wzrostu
M ≈ xn/2 ≈ x 100 /2 ≈ x50 ≈ 180 [cm] 100 bo n = ∑ ni =100%
najbliżej 50 jest 30
50% badanych studentów ma wzrost 180 cm lub mniej a pozostałe 50% badanych studentów ma wzrost 180 cm lub więcej.
Q 1.4 ≈ xn/4 ≈ x 100/4 ≈ x25 ≈ 170 [cm] bo x25 = 170 cm
25% badanych studentów ma wzrost 170 cm lub mniej a pozostałe 75% badanych studentów ma wzrost 170 cm lub więcej.
Q3.4 ≈ X 3 * n ≈ x 3 * 100≈ x300 ≈ x75 ≈ 180 [cm] bo x75 = 180 cm
44 4
75% badanych studentów ma wzrost 180 cm lub mniej a pozostałe 25% badanych studentów ma wzrost 180 cm lub więcej
Obliczyć klasyczną, absolutną miarę zróżnicowania (średnią arytmetyczną)
S (x) = √ x2 - (x)2 gdzie ∑ xi2 * ni aby to obliczyć należy obliczyć xi -* ni a wyniki zsumować
x2 = n poczym obliczyć xi2 * ni i wyniki też zsumować a następnie podstawiamy:
∑ xi * ni 17750
x = n = 100 = 177,5 [cm] bo ∑ xi * ni = 17750/100 = 177,5
∑ xi2 * ni 3155250
następnie podstawiamy do x2 = n = 100 = 31552,5 bo ∑ xi2 * ni = 3155250/100 = 31552,5
(…)
… zamieszkującej miasta województwa zachodniopomorskiego. Otrzymano następujące dane w tys. xi
ni
nsk
Do 1
100
0 + 100 = 100
2 - 3
80
100 + 80 = 180
4 - 5
50
180 + 50 = 230
6 - 7
30
230 + 30 = 260
8 - 9
20
260 + 20 = 280
∑ 280
określić zbiorowość, jednostkę i cechę statystyczną
Zbiorowością statystyczną są miasta województwa zachodniopomorskiego zbadane w dniu 31. XII. 1999r.;
Jednostką statystyczną jest każde…
… - średnia arytmetyczna- ma interpretację
D - domianta;
M - mediana; mają interpretację
Q1.3;; Q3.4 - kwartyle
MIARA DYSPERSJI KLASYCZNA
MIARA DYSPERSJI POZYCYJNA
ABSOLUTNA S(x) - odchylenie standardowe - ma interpretacę
Q—odchylenie ćwiartkowe - mają interpretację; pojawia się słowo w zawężonym
STOSUNKOWA VS- odchylenie standardowe- ma interpretację
VQ - odchylenie ćwiartkowe - ma interpretację; pojawia…
… pracowników względem siebie
Miary zróżnicowania to: S(x),- średnia arytmetyczna- odchylenie ćwiartkowe, VS,- odchylenie standardowe, VQ - pozycyjny współczynnik zmienności - miara stosunkowa niemianowana.
S(x) = √S2(x) = √ 0,0324 = 0,18 [tys]
Interpretacja Wynagrodzenie pracowników różni się od średniej arytmetycznej przeciętnie o +, - 0,18 [tys] zł.
S(x) 0,18
VS = x * 100% = 0,96 * 100% = 18,75…
... zobacz całą notatkę






Komentarze użytkowników (0)