To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
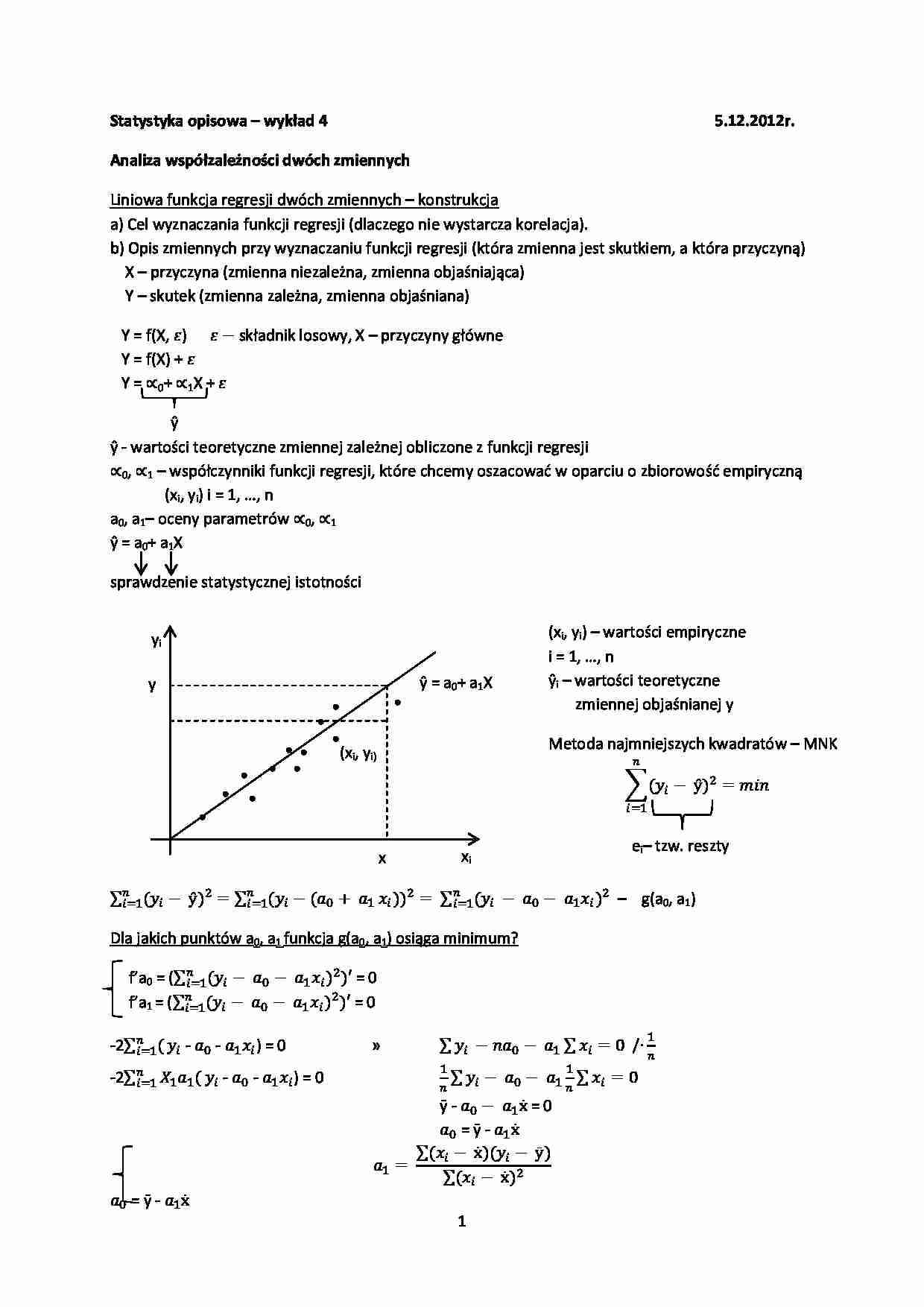


S tatystyka opisowa - wykład 4 5.12.2012r. Analiza współzależności dwóch zmiennych Liniowa funkcja regresji dwóch zmiennych - konstrukcja a) Cel wyznaczania funkcji regresji (dlaczego nie wystarcza korelacja). b) Opis zmiennych przy wyznaczaniu funkcji regresji (która zmienna jest skutkiem, a która przyczyną) X - przyczyna (zmienna niezależna, zmienna objaśniająca) Y - skutek (zmienna zależna, zmienna objaśniana)
Y = f(X, ) składnik losowy, X - przyczyny główne Y = f(X) + Y = 0 + 1 X + ŷ - wartości teoretyczne zmiennej zależnej obliczone z funkcji regresji 0 , 1 - współczynniki funkcji regresji, które chcemy oszacować w oparciu o zbiorowość empiryczną (x i , y i ) i = 1, …, n a 0 , a 1 - oceny parametrów 0 , 1 ŷ = a 0 + a 1 X
sprawdzenie statystycznej istotności
• •
•
•
•
•
•
•
•
•
•
•
•
y i x i x
y
ŷ = a 0 + a 1 X
(x i , y i) - g(a 0 , a 1 )
Dla jakich punktów a 0 , a 1 funkcja g(a 0 , a 1 ) osiąga minimum? f'a 0 = ( = 0 f'a 1 = ( = 0
-2 - - ) = 0 » / -2 - - ) = 0 ȳ - = 0 = ȳ - = ȳ - d) wyjaśnienie interpretacji parametrów równania regresji W przypadku funkcji regresji interpretacji podlega tylko współczynnik a 1 . ŷ = ŷ k - ŷ p = (a 0 + a 1 x k ) - (a 0 + a 1 x p ) = a 1 (x k - x p )
ŷ = a 1 x Jeśli x = 1 » ŷ = a 1 Współczynnik kierunkowy a 1 informuje o ile przeciętnie zmieni się zmienna objaśniająca ŷ (jeśli a 1 0 to ta zmiana będzie wzrostem, jeśli a 1
(…)
…
Statystyka opisowa - wykład 4 5.12.2012r.
Analiza współzależności dwóch zmiennych
Liniowa funkcja regresji dwóch zmiennych - konstrukcja a) Cel wyznaczania funkcji regresji (dlaczego nie wystarcza korelacja). b) Opis zmiennych przy wyznaczaniu funkcji regresji (która zmienna jest skutkiem, a która przyczyną) X - przyczyna (zmienna niezależna, zmienna objaśniająca) Y - skutek (zmienna zależna…
…) współczynnik determinacji (R2) i zbieżności (brak determinacji - ϕ2) - konstrukcja i interpretacja Yi = ŷi + ei Sy2 = Sŷ2 + Se2 /: Sy2 1 = + 1 = R2 + ϕ2 » 100% = R2 100% + ϕ2 100% » R2 = r2 R2 = ϕ2 = Interpretacja Współczynnik determinacji R2 informuje w jakim % zmienność zmiennej objaśnianej y jest wyjaśniona regresją, czyli wynika ze zmienności zmiennej objaśniającej x. ϕ2 informuje w jakim % zmienność zmiennej objaśnianej y nie wynika z funkcji regresji, ale z innych czynników nieuwzględnionych w regresji.
Jeżeli mamy regresję liniową ŷi = a0 + a1xi , to: R2 = r2xy » ϕ2 = 1 - r2xy a) X - zmienna niezależna Y - zmienna zależna R2 = r2xy Se = b) X - zmienna zależna Y - zmienna niezależna R2 = r2xy Se = Im lepsze dopasowanie tym kąt pomiędzy funkcjami jest mniejszy.
Korelacja liniowa (represja liniowa) R2…
... zobacz całą notatkę






Komentarze użytkowników (0)