To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
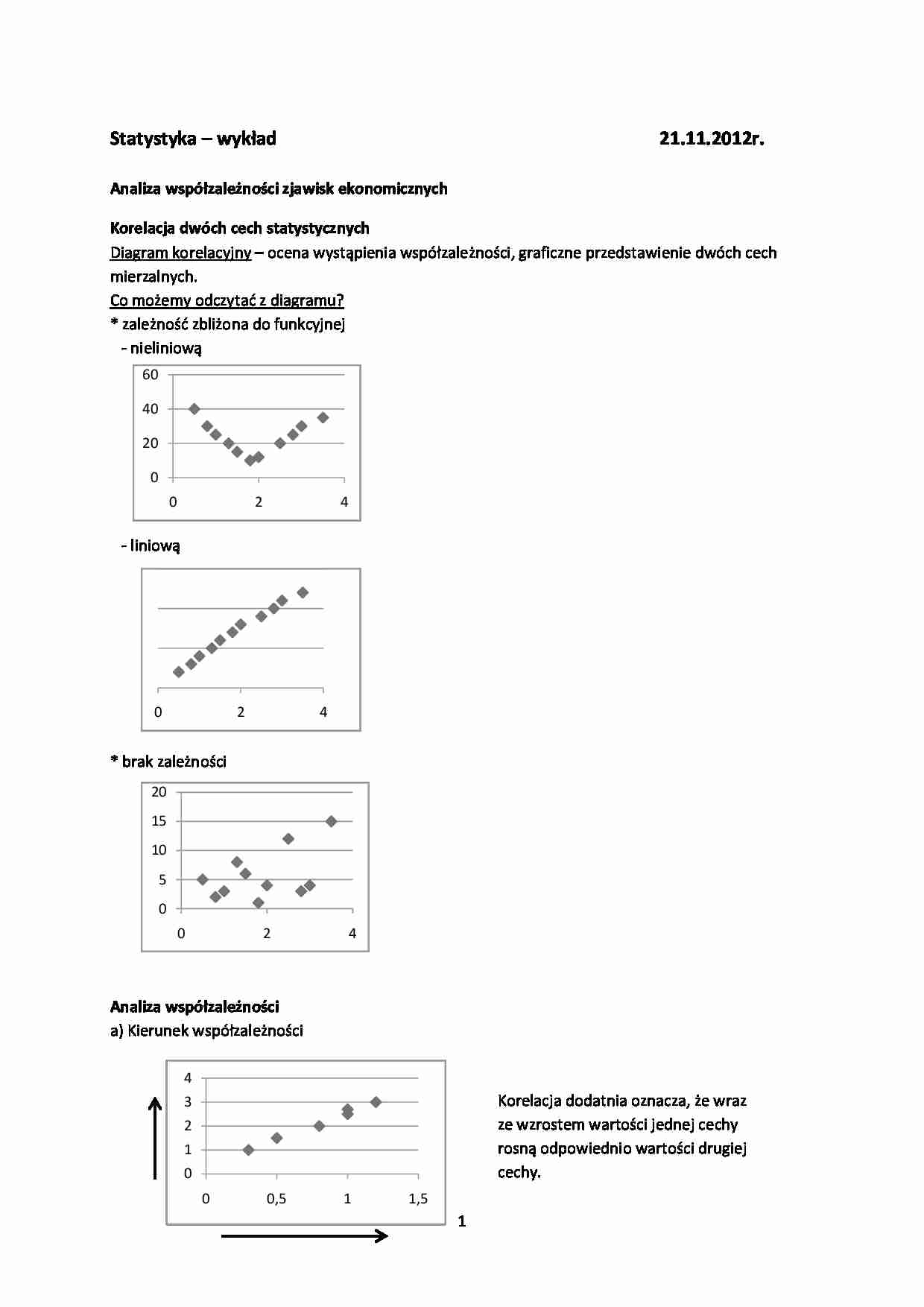


S tatystyka - wykład 21.11.2012r. Analiza współzależności zjawisk ekonomicznych Korelacja dwóch cech statystycznych Diagram korelacyjny - ocena wystąpienia współzależności, graficzne przedstawienie dwóch cech mierzalnych. Co możemy odczytać z diagramu? * zależność zbliżona do funkcyjnej - nieliniową - liniową * brak zależności Analiza współzależności a) Kierunek współzależności b) siła współzależności Tam, gdzie rozrzut jest mniejszy, tam silniejsza jest współzależność. Miary korelacji dwóch cech ilościowych * współczynnik kowariancji c(X,Y) = cov(X,Y) - konstrukcja miary cov(X, Y) = I II III IV y i - ȳ 0 y i ȳ y i - ȳ 0 x i ẋ ẋ ȳ (x i - ẋ)(y i - ȳ) 0 I i III (x i - ẋ)(y i - ȳ) 0 II i IV (x i - ẋ)(y i - ȳ)
(…)
…. Sposób postępowania: * nadanie rang cechom jakościowym (sztuczne wartości - liczby naturalne) oraz określenie maksymalnej wartości (pozytywnej: np. 1 - max) rxi, ryi - odpowiednie rangi cechy X i Y * wzór: rs - Interpretacja: współczynnik korelacji rang ma taką samą interpretację jak współczynnik korelacji Pearsona (rxy). - Ocena zgodności uporządkowania rang badanych cech (kierunek) a) rs > 0 - tzn. korelacja…
… współzależności
Tam, gdzie rozrzut jest mniejszy, tam silniejsza jest współzależność.
Miary korelacji dwóch cech ilościowych * współczynnik kowariancji c(X,Y) = cov(X,Y) - konstrukcja miary cov(X, Y) = I
II
III
IV
yi - ȳ > 0 yi > ȳ
yi - ȳ < 0 yi < ȳ
xi - ẋ < 0 xi < ẋ
xi - ẋ > 0 xi > ẋ
ẋ
ȳ
(xi - ẋ)(yi - ȳ) > 0
I i III (xi - ẋ)(yi - ȳ) > 0
II i IV (xi - ẋ)(yi - ȳ) < 0
* współczynnik korelacji Pearsona r(X, Y) =rXY…
... zobacz całą notatkę






Komentarze użytkowników (0)