To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
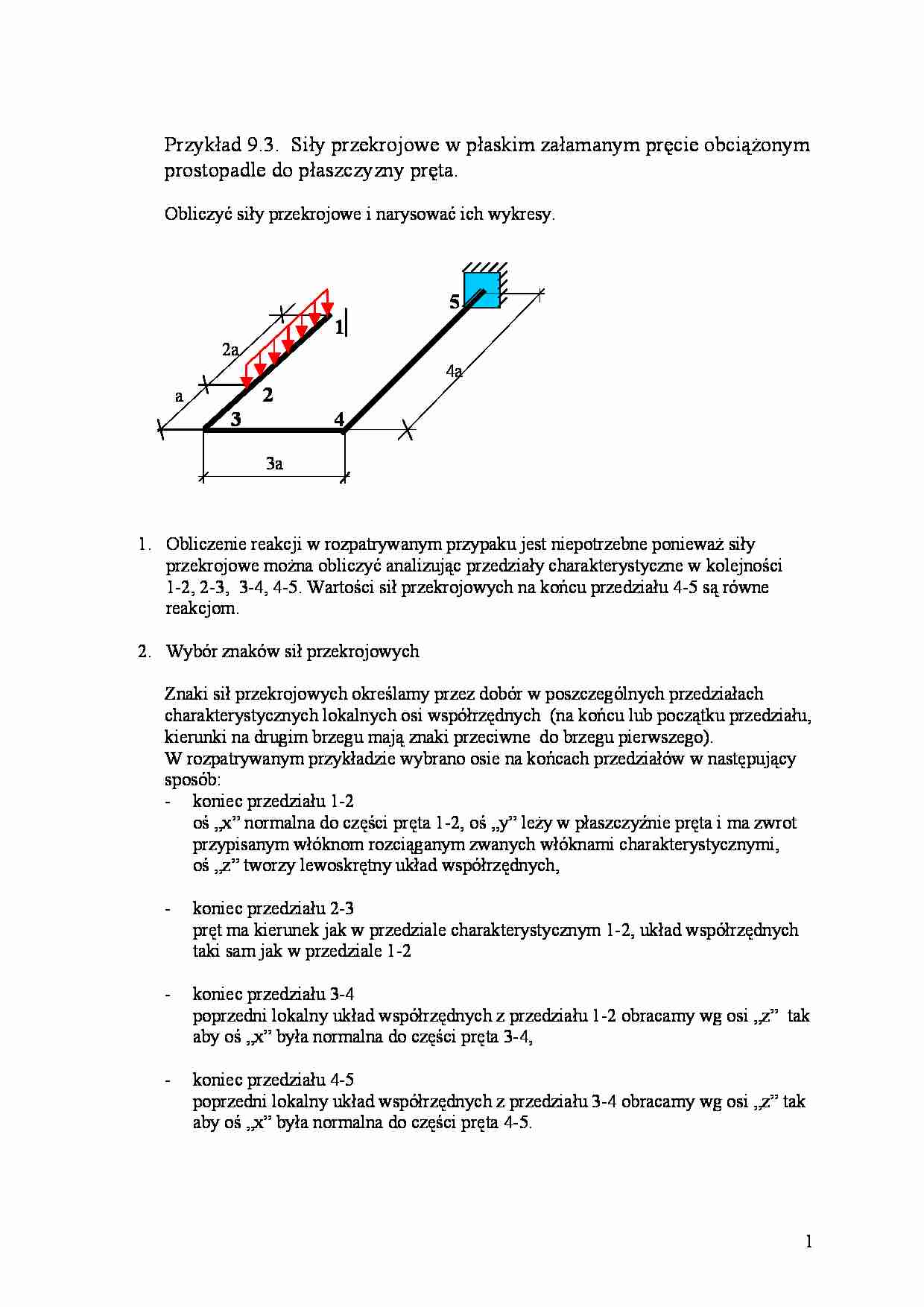


Przykład 9.3. Siły przekrojowe w płaskim załamanym pręcie obciążonym prostopadle do płaszczyzny pręta. Obliczyć siły przekrojowe i narysować ich wykresy. 5 1 2a 4a a 2 3 4 3a 1. Obliczenie reakcji w rozpatrywanym przypaku jest niepotrzebne ponieważ siły przekrojowe można obliczyć analizując przedziały charakterystyczne w kolejności 1-2, 2-3, 3-4, 4-5. Wartości sił przekrojowych na końcu przedziału 4-5 są równe reakcjom. 2. Wybór znaków sił przekrojowych Znaki sił przekrojowych określamy przez dobór w poszczególnych przedziałach charakterystycznych lokalnych osi współrzędnych (na końcu lub początku przedziału, kierunki na drugim brzegu mają znaki przeciwne do brzegu pierwszego). W rozpatrywanym przykładzie wybrano osie na końcach przedziałów w następujący sposób: - koniec przedziału 1-2 oś „x” normalna do części pręta 1-2, oś „y” leży w płaszczyźnie pręta i ma zwrot przypisanym włóknom rozciąganym zwanych włóknami charakterystycznymi, oś „z” tworzy lewoskrętny układ współrzędnych, - koniec przedziału 2-3 pręt ma kierunek jak w przedziale charakterystycznym 1-2, układ współrzędnych taki sam jak w przedziale 1-2 - koniec przedziału 3-4 poprzedni lokalny układ współrzędnych z przedziału 1-2 obracamy wg osi „z” tak aby oś „x” była normalna do części pręta 3-4,
(…)
… przedziałów charakterystycznych
Pręt załamany z obciążeniem działającym prostopadle do płaszczyzny pręta (z sześciu sił
przekrojowych, trzy wielkości są zerowe – siła normalna, moment gnący o wektorze w
prostopadłym do płaszczyzny pręta, oraz siła tnąca w płaszczyźnie ramy).
Siły przekrojowe w każdym przedziale charakterystycznym dla pozostałych (niezerowych)
składowych wyznaczamy z warunków równowagi…
... zobacz całą notatkę






Komentarze użytkowników (0)