To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
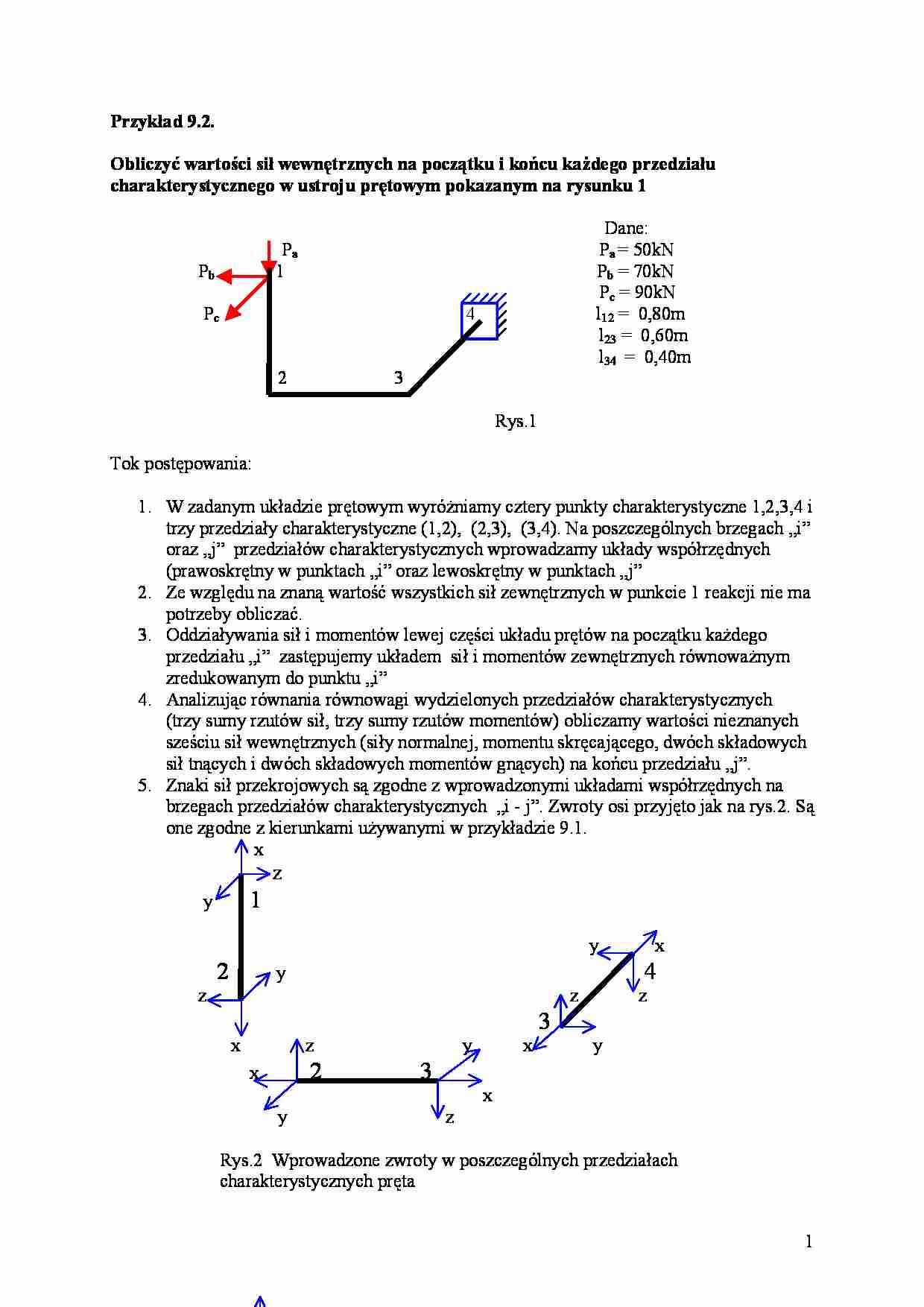

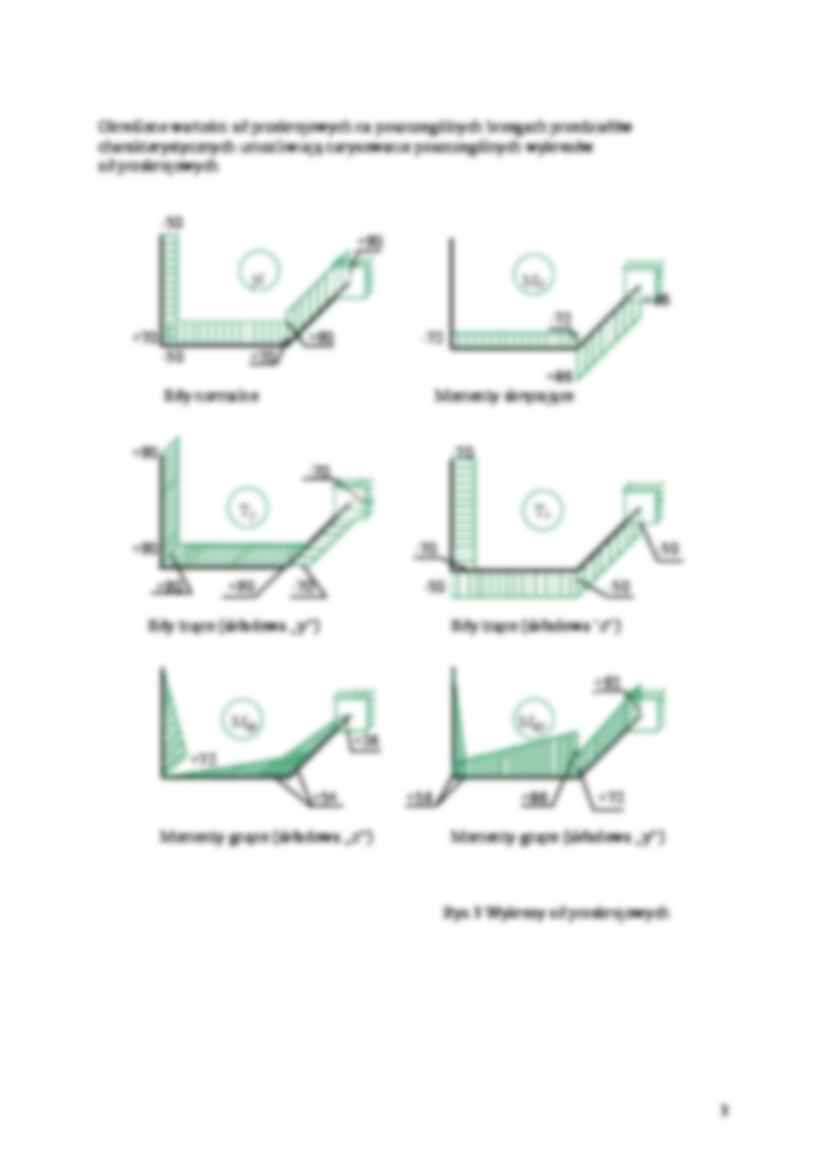
Przykład 9.2. Obliczyć wartości sił wewnętrznych na początku i końcu każdego przedziału charakterystycznego w ustroju prętowym pokazanym na rysunku 1 Dane: Pa Pa = 50kN Pb 1 Pb = 70kN Pc = 90kN Pc 4 l12 = 0,80m l23 = 0,60m l34 = 0,40m 2 3 Rys.1 Tok postępowania: 1. W zadanym układzie prętowym wyróżniamy cztery punkty charakterystyczne 1,2,3,4 i trzy przedziały charakterystyczne (1,2), (2,3), (3,4). Na poszczególnych brzegach „i” oraz „j” przedziałów charakterystycznych wprowadzamy układy współrzędnych (prawoskrętny w punktach „i” oraz lewoskrętny w punktach „j” 2. Ze względu na znaną wartość wszystkich sił zewnętrznych w punkcie 1 reakcji nie ma potrzeby obliczać. 3. Oddziaływania sił i momentów lewej części układu prętów na początku każdego przedziału „i” zastępujemy układem sił i momentów zewnętrznych równoważnym zredukowanym do punktu „i” 4. Analizując równania równowagi wydzielonych przedziałów charakterystycznych (trzy sumy rzutów sił, trzy sumy rzutów momentów) obliczamy wartości nieznanych sześciu sił wewnętrznych (siły normalnej, momentu skręcającego, dwóch składowych sił tnących i dwóch składowych momentów gnących) na końcu przedziału „j”. 5. Znaki sił przekrojowych są zgodne z wprowadzonymi układami współrzędnych na brzegach przedziałów charakterystycznych „i - j”. Zwroty osi przyjęto jak na rys.2. Są one zgodne z kierunkami używanymi w przykładzie 9.1. x z
(…)
… równoważnym
zredukowanym do punktu „i”
4. Analizując równania równowagi wydzielonych przedziałów charakterystycznych
(trzy sumy rzutów sił, trzy sumy rzutów momentów) obliczamy wartości nieznanych
sześciu sił wewnętrznych (siły normalnej, momentu skręcającego, dwóch składowych
sił tnących i dwóch składowych momentów gnących) na końcu przedziału „j”.
5. Znaki sił przekrojowych są zgodne z wprowadzonymi…
... zobacz całą notatkę






Komentarze użytkowników (0)