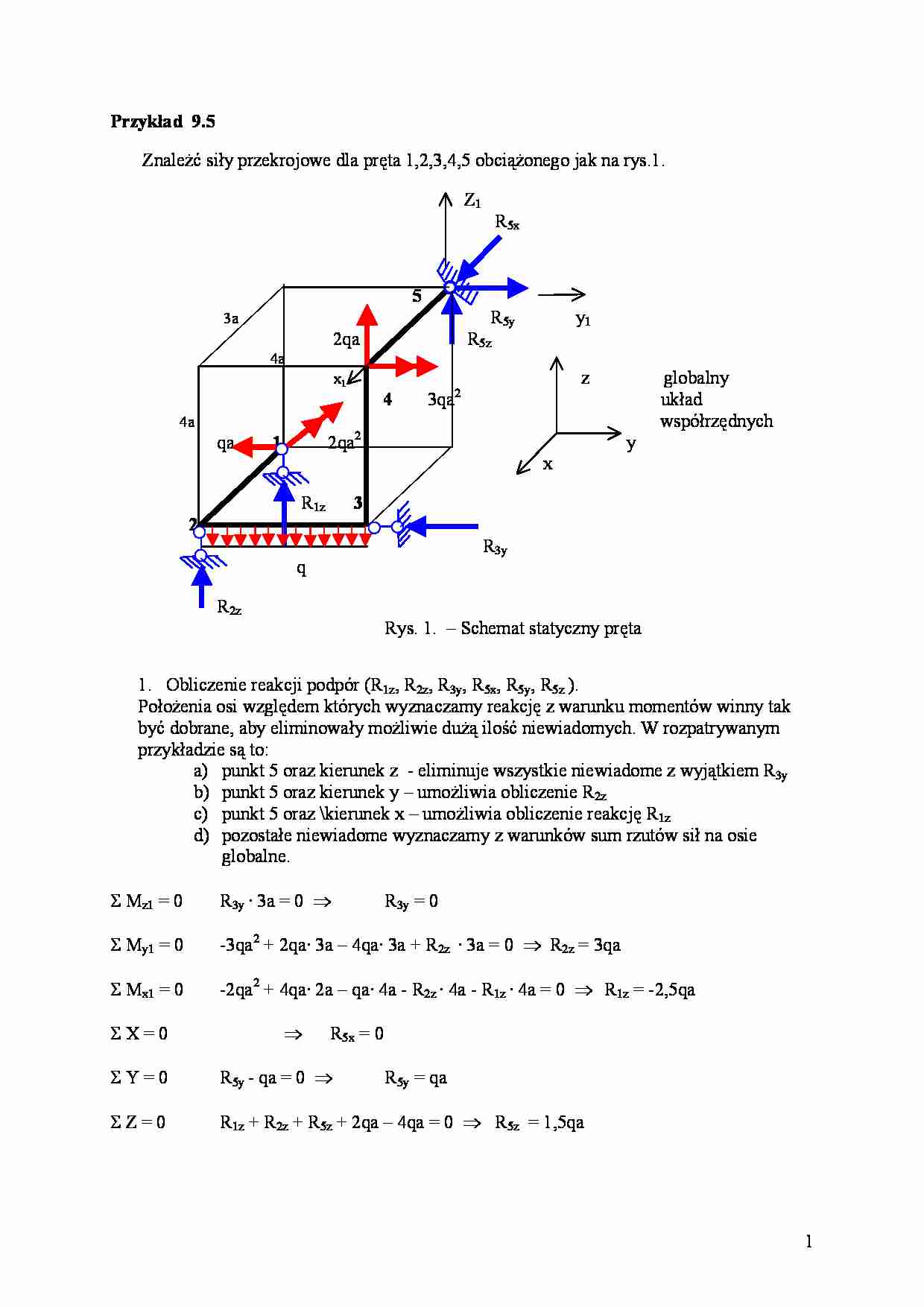
Przykład 9.5 Znależć siły przekrojowe dla pręta 1,2,3,4,5 obciążonego jak na rys.1. Z1 R5x 5 3a R5y y1 2qa R5z 4a x1 z globalny 4 3qa 2 układ 4a współrzędnych qa 1 2qa2 y x R1z 3 2 R3y q R2z Rys. 1. – Schemat statyczny pręta 1. Obliczenie reakcji podpór (R1z, R2z, R3y, R5x, R5y, R5z ). Położenia osi względem których wyznaczamy reakcję z warunku momentów winny tak być dobrane, aby eliminowały możliwie dużą ilość niewiadomych. W rozpatrywanym przykładzie są to: a) punkt 5 oraz kierunek z - eliminuje wszystkie niewiadome z wyjątkiem R3y b) punkt 5 oraz kierunek y – umożliwia obliczenie R2z c) punkt 5 oraz \kierunek x – umożliwia obliczenie reakcję R1z d) pozostałe niewiadome wyznaczamy z warunków sum rzutów sił na osie globalne. Σ Mz1 = 0 R3y · 3a = 0 ⇒ R3y = 0 Σ My1 = 0 -3qa2 + 2qa· 3a – 4qa· 3a + R2z · 3a = 0 ⇒ R2z = 3qa Σ Mx1 = 0 -2qa2 + 4qa· 2a – qa· 4a - R2z · 4a - R1z · 4a = 0 ⇒ R1z = -2,5qa Σ X = 0 ⇒ R5x = 0
(…)
…
Obliczenie maksymalnego momentu w przedziale 2-3
- miejsce zerowe siły tnącej
0,5qa/xo = 4,0qa/4a ⇒ xo = 0,5a
- obliczenie momentu maksymalnego
Mmax = 2qa2 + 0,5qa · 0,5a - 0,5qa · 0,25a = 2,125qa2.
Wykresy sił przekrojowych wyznaczone na podstawie tabeli nr1 pokazano na rys.4
3
2,5qa -3qa2
N Ms
+2qa2
-3qa2
+qa +2,5qa +2qa2
qa
+4,5qa2 +4,5qa2
Wykres sił normalnych Wykres momentów skręcających
-qa
-qa -3qa2…
…]
Tz [qa]
Mgy [qa2]
0
2,0
2,5
0
1,0
0
0
2,0
2,5
-7,5
1,0
-3,0
1,0
4,5
-0,5
2,0
0
-3,0
1,0
4,5
3,5
-4,0
0
-3,0
Przedział
charakterystyczny
3-4
2,5
-3,0
-1,0
-4,0
0
7,5
2,5
-3,0
-1,0
0
0
7,5
Przedział
charakterystyczny
4-5
0
0
-1,0
-3,0
-1,5
4,5
0
0
-1,0
0
1,5
0
Obliczenie maksymalnego momentu w przedziale 2-3
-
miejsce zerowe siły tnącej
0,5qa/xo = 4,0qa/4a
⇒ xo = 0,5a
obliczenie momentu maksymalnego…
... zobacz całą notatkę





Komentarze użytkowników (0)