To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
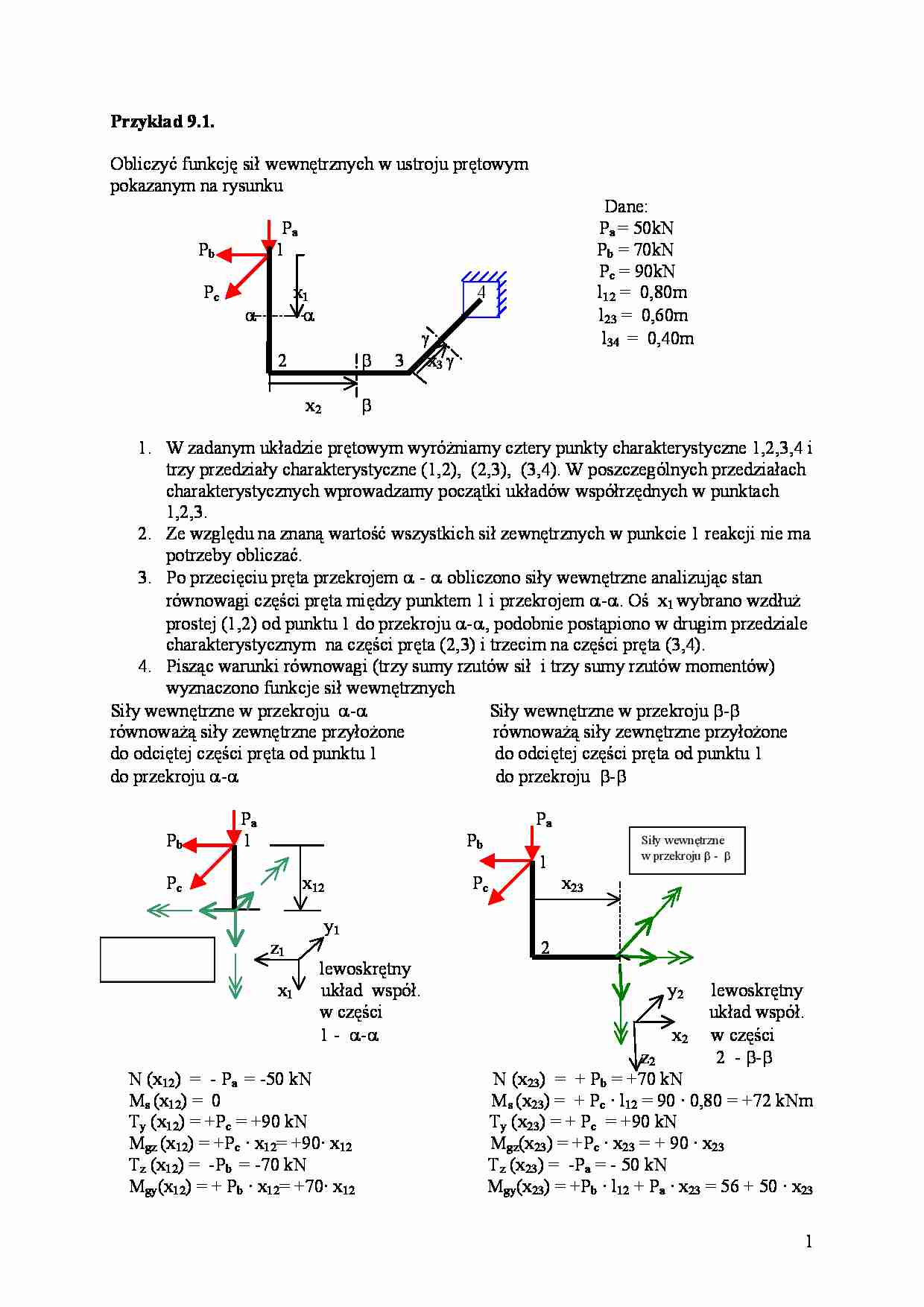

Przykład 9.1. Obliczyć funkcję sił wewnętrznych w ustroju prętowym pokazanym na rysunku Dane: Pa Pa = 50kN Pb 1 Pb = 70kN Pc = 90kN Pc x1 4 l12 = 0,80m α α l23 = 0,60m γ l34 = 0,40m 2 β 3 x3 γ x2 β 1. W zadanym układzie prętowym wyróżniamy cztery punkty charakterystyczne 1,2,3,4 i trzy przedziały charakterystyczne (1,2), (2,3), (3,4). W poszczególnych przedziałach charakterystycznych wprowadzamy początki układów współrzędnych w punktach 1,2,3. 2. Ze względu na znaną wartość wszystkich sił zewnętrznych w punkcie 1 reakcji nie ma potrzeby obliczać. 3. Po przecięciu pręta przekrojem α - α obliczono siły wewnętrzne analizując stan równowagi części pręta między punktem 1 i przekrojem α-α. Oś x1 wybrano wzdłuż prostej (1,2) od punktu 1 do przekroju α-α, podobnie postąpiono w drugim przedziale charakterystycznym na części pręta (2,3) i trzecim na części pręta (3,4). 4. Pisząc warunki równowagi (trzy sumy rzutów sił i trzy sumy rzutów momentów) wyznaczono funkcje sił wewnętrznych Siły wewnętrzne w przekroju α-α Siły wewnętrzne w przekroju β-β równoważą siły zewnętrzne przyłożone równoważą siły zewnętrzne przyłożone do odciętej części pręta od punktu 1 do odciętej części pręta od punktu 1 do przekroju α-α do przekroju β-β
... zobacz całą notatkę




Komentarze użytkowników (0)