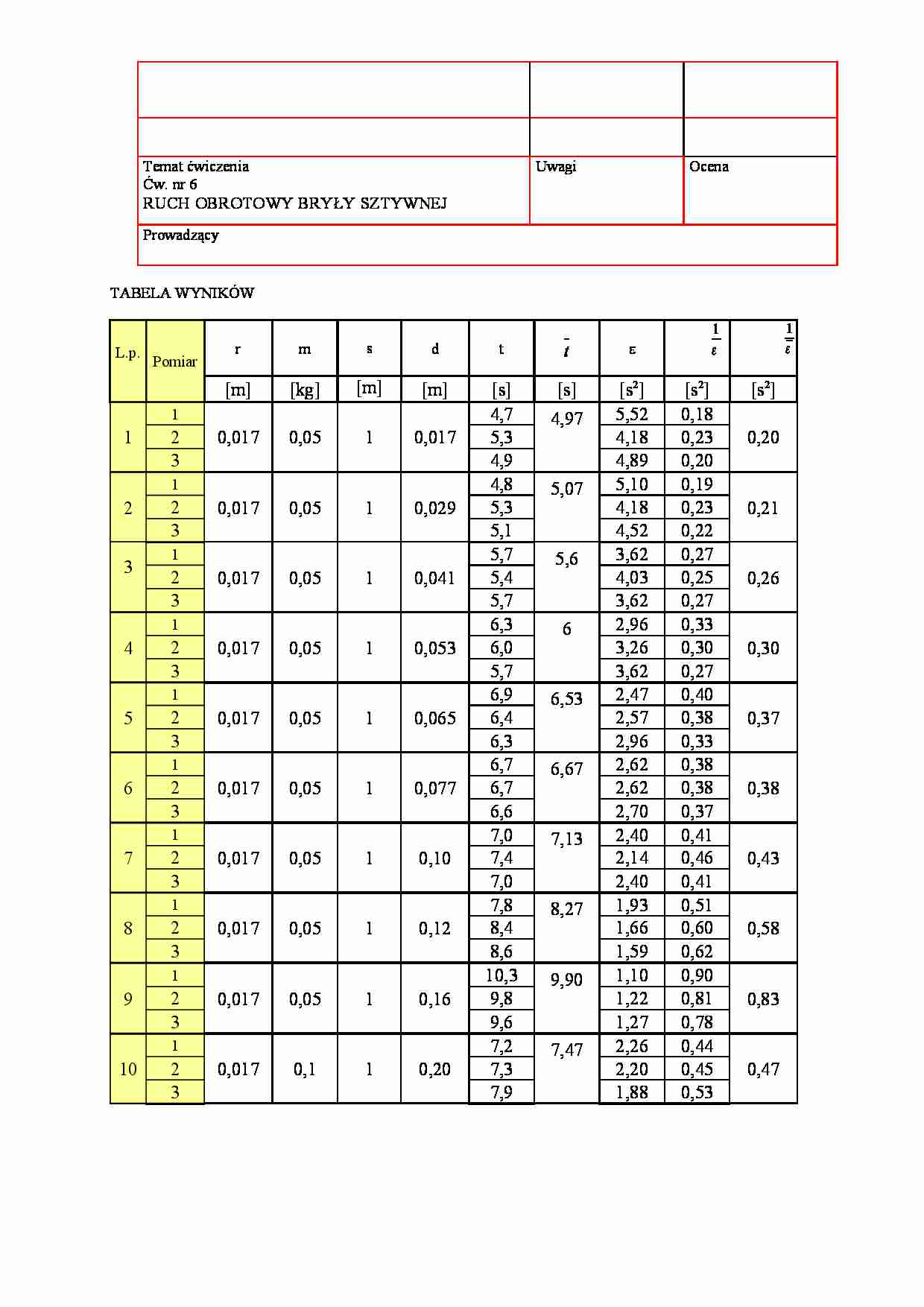
Temat ćwiczenia Ćw. nr 6 RUCH OBROTOWY BRYŁY SZTYWNEJ Uwagi Ocena Prowadzący TABELA WYNIKÓW L.p. Pomiar r m s d t t ε [m] [kg] [m] [m] [s] [s] [s2] [s2] [s2] 1 1 0,017 0,05 1 0,017 4,7 4,97 5,52 0,18 0,20 2 5,3 4,18 0,23 3 4,9 4,89 0,20 2 1 0,017 0,05 1 0,029 4,8 5,07 5,10 0,19 0,21 2 5,3 4,18 0,23 3 5,1 4,52 0,22 3 1 0,017 0,05 1 0,041 5,7 5,6 3,62 0,27 0,26 2 5,4 4,03 0,25 3 5,7 3,62 0,27 4 1 0,017 0,05 1 0,053 6,3 6 2,96 0,33 0,30 2 6,0 3,26 0,30 3 5,7 3,62 0,27 5 1 0,017 0,05 1 0,065 6,9 6,53 2,47 0,40 0,37 2 6,4 2,57 0,38 3 6,3 2,96 0,33 6 1 0,017 0,05 1 0,077 6,7 6,67 2,62 0,38 0,38 2 6,7 2,62 0,38 3 6,6 2,70 0,37 7 1 0,017 0,05 1 0,10 7,0 7,13 2,40 0,41 0,43 2 7,4 2,14 0,46 3 7,0 2,40 0,41 8 1 0,017 0,05 1 0,12 7,8 8,27 1,93 0,51 0,58 2 8,4 1,66 0,60 3 8,6 1,59 0,62 9 1 0,017 0,05 1 0,16 10,3 9,90 1,10 0,90 0,83 2 9,8 1,22 0,81 3 9,6 1,27 0,78 10 1 0,017 0,1 1 0,20 7,2 7,47 2,26 0,44 0,47 2 7,3 2,20 0,45 3 7,9 1,88 0,53 ε 1 ε 1 Wykonanie pomiarów . Badanie przeprowadzam wykorzystując wahadło Oberbecka. 1. Ciężarki ustawiam w jak najmniejszej odległości od osi obrotu, a na nici przełożonej przez bloczek zawieszam odważnik o masie 50,1 g. 2. Trzykrotnie odmierzam czas opadania odważnika na drodze 1 m (s). Pomiar powtarzam dla 10 różnych odległości ciężarków od osi obrotu (d). 3. Wyniki zestawiam w tabeli. 4. Następnie obliczam przyśpieszenie kątowe korzystając ze wzoru: 2 2 t r s r a ⋅ ⋅ = = ε ⋅ 2 s m m gdzie: t – czas opadania na drodze s Obliczenia: ( ) 32 , 5 7 , 4 017 , 0 1 2 2 11 = ⋅ ⋅ = ε ( ) 18 , 4 3 , 5 017 , 0 1 2 2 12 = ⋅ ⋅ = ε ( ) 89 , 4 9 , 4 017 , 0 1 2 2 13 = ⋅ ⋅ = ε ( ) 10 , 5 8 , 4 017 , 0 1 2 2 21 = ⋅ ⋅ = ε ( ) 18 , 4 3 , 5 017 , 0 1 2 2 22 = ⋅ ⋅ = ε ( ) 452 1 , 5 017 , 0 1 2 2 23 = ⋅ ⋅ = ε ( ) 62 , 3 7 , 5 017 , 0 1 2 2 31 = ⋅ ⋅ = ε ( ) 03 , 4 4 , 5 017 , 0 1 2 2 32 = ⋅ ⋅ = ε ( ) 62 , 3 7 , 5 017 , 0 1 2 2 33 = ⋅
... zobacz całą notatkę





Komentarze użytkowników (0)