To tylko jedna z 6 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


17. Ruch ładunku w polu elektromagnetycznym. Prąd elektryczny
Wybór i opracowanie Marek Chmielewski
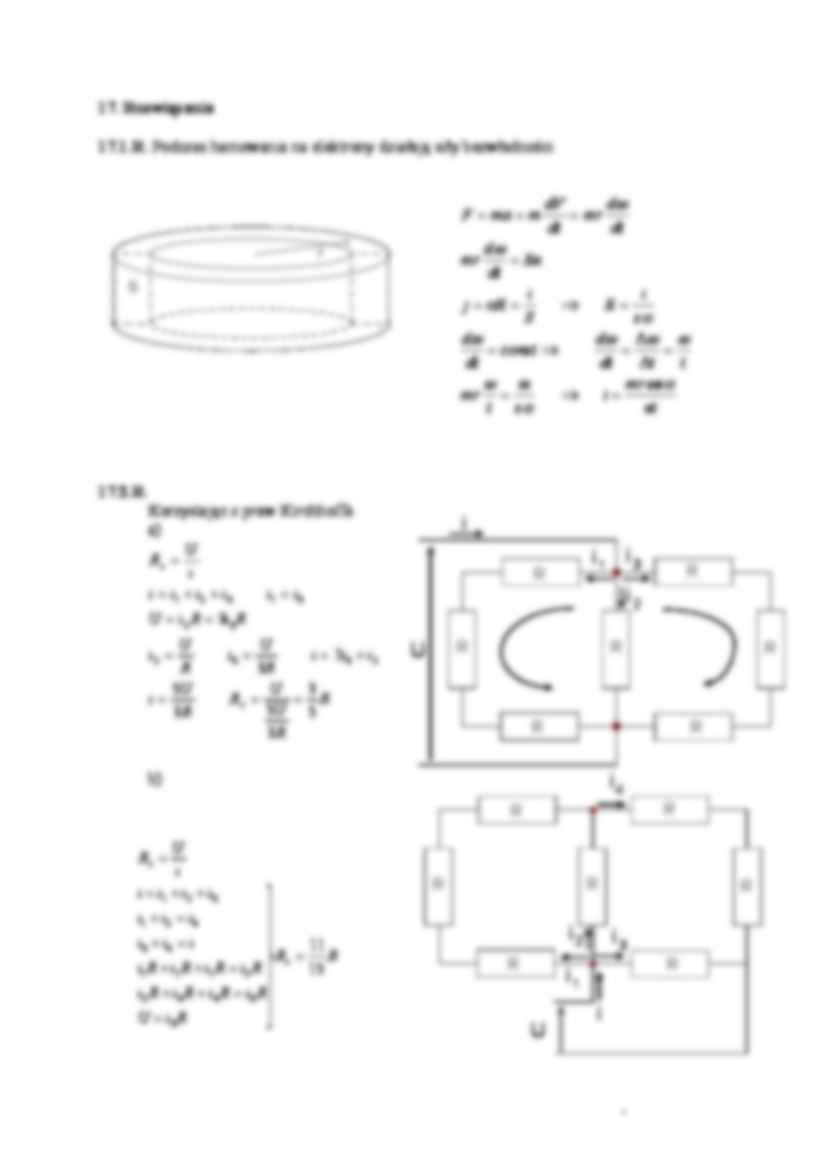
17.1. Z aluminiowego pręta o przekroju poprzecznym S wykonano zamknięty pierścień o
promieniu r. Ten pierścień wiruje z prędkością kątową ω wokół osi przechodzącej przez
jego środek prostopadle do płaszczyzny pierścienia. Ruch pierścienia został gwałtownie
zatrzymany. Przyjmując, że w czasie hamowania trwającego t przyspieszenie kątowe
było stałe, oblicz natężenie prądu płynącego podczas hamowania ruch. Przewodnictwo
aluminium wynosi σ.
17.2. Jednakowe oporniki o oporach R każdy połączono jak na rysunku. Oblicz opór
zastępczy układu między punktami A i B oraz B i C.
A
C
B
17.3.Fragment rozgałęzionego obwodu składa się z trzech oporników połączonych w trójkąt.
Znaleźć oporność R1,R2,R3 elementów gwiazdy, która wmontowana w obwód na miejsce
trójkąta będzie równoważna trójkątowi.
R3
r2
r1
R2
R1
r3
17.4.Pyłek o masie m i ładunku q spada w próżni w polu płaskiego kondensatora,
naładowanego do napięcia U. Okładki kondensatora są ustawione pionowo i oddalone od
siebie o d. Jaka powinna być wysokość okładek, by pyłek nie uderzył o okładkę. W
chwili początkowej pyłek znajdowała się tuż przy powierzchni jednej z okładek.
17.5.W jednorodnym polu magnetycznym o indukcji B z tego samego punktu wybiegają dwie
cząstki o masie m i ładunku Q każda, z tymi samymi prędkościami, ale różnie
skierowanymi. Wektor prędkość pierwszej cząstki V1 tworzy z kierunkiem wektora B
kąt α, a wektor prędkości drugiej cząstki V2 – kąt β, przy czym αβ. W jakim odstępie
czasu t po pierwszej powinna wybiec druga cząstka, aby nastąpiło spotkanie. Wektory
V1, V2 i B leżą w jednej płaszczyźnie.
17.6.Oblicz, jaka masę m musiałaby mieć cząstka naładowana ładunkiem elementarnym e aby
w próżni okrążała kulę ziemską wzdłuż równika magnetycznego, jeżeli składowa
pozioma wektora indukcji magnetycznej ma średnia wartość Bs, a prędkość cząstki
wynosi V.
17.7.Elektron o energii kinetycznej E wlatuje w jednorodne pole magnetyczne o indukcji B.
Oblicz promień okręgu, po którym będzie krążył elektron w tym polu. Ładunek
elektronu wynosi q, masa m. Wektor prędkości elektronu V jest prostopadły do wektora
B. Jaka będzie częstotliwość obiegu elektronu po orbicie? Zbadać, jak zależy
częstotliwość obiegu elektronu po orbicie od jego energii kinetycznej.
17. Rozwiązania
17.1.R. Podczas hamowania na elektrony działają siły bezwładności
F = ma = m
dV
dω
= mr
dt
dt
dω
= Ee
dt
i
j = σE =
⇒
S
dω
= const ⇒
dt
ω ie
mr =
⇒
t sσ
r
mr
S
17.2.R.
Korzystając z praw Kirchhoffa
a)
U
Rz =
i
i = i1 + i2 + i3
i1 = i3
E=
sσ
dω ∆ω ω
=
=
∆t
dt
t
mrωsσ
i=
et
i
i1 i3
R
U
R
5U
i=
3R
U
i = 2i3 + i2
3R
3
U
Rz =
= R
5U 5
3R
i3 =
R
U
R
R
R
R
i4
b)
R
R
U
i
i = i1 + i2 + i3
R
i2
U = i2 R = 3i3 R
i2 =
i
Rz =
i1 + i2 = i4
i3 + i4 = i
11
Rz = R
i1 R + i1 R + i1 R = i2 R
15
i2 R + i4 R + i4 R = i3 R
U = i3 R
R
R
i2
R
i3
R
i1
U
R
i
Uwaga w obu przypadkach można wyznaczyć rezystancje zastępczą szukając oporu
poszczególnych gałęzi obwodów.
b)
2R
3R
R
R
R
3R
3R
a)
17.3.R.
IB
IB
B
IA
R3
r2
r1
R2
IC
A
r3
B
C
R1
A
IA
C
IC
Zamiennik musi działać tak aby prądy jak i spadki napięć w jednym jak i drugim układzie
były takie same więc:
Dla układu trójkąta
IA =
U AB U AC
+
r1
r3
IC =
U BC U AC
+
r2
r3
IC =
1 1
U AB
+ U BC +
r r
r3
3
2
U AC = U AB + U BC
1 1 U
I A = U AB + + BC
r r r
3
1 3
Dla układu gwiazdy
U AB = I A R2 + I B R3
U BC = − I B R3 + I C R1
I B = I A − IC
U AB = I A ( R2 + R3 ) − I C1 R3
U BC = − I A R3 + I C ( R1 + R3 )
Układy te należy rozwiązać ze względu na IA oraz IC
IA =
( R1 + R3 )U AB
R3U BC
+
R1 R2 + R1 R3 + R2 R3 R1 R2 + R1 R3 + R2 R3
IC =
R3U AB
( R2 + R3 )U BC
+
R1 R2 + R1 R3 + R2 R3 R1 R2 + R1 R3 + R2 R3
Porównując wyrażenia na prąd dla trójkąta i gwiazdy można wyznaczyć szukane
zależności przez przyrównanie wyrażeń przy UAB i UBC.
r3 =
R1 R2 + R1 R3 + R2 R3
R3
W analogiczny sposób obliczamy kolejne zależności. Łatwo zauważyć regularność w
uzyskiwaniu tych wyrażeń.
r1 =
R1 R2 + R1 R3 + R2 R3
R1
r2 =
17.4.R.
Rozpatrujemy układ równań
R1 R2 + R1 R3 + R2 R3
R2
axt 2
x(t ) =
+ V0 x t + x0
2
a yt 2
y (t ) =
+ V0 y t + y0
2
Z warunków zadania otrzymujemy:
V0x=V0y=x0=y0=0
U
Fe = Eq = q
d
ay = g
y (t k ) = l max =
mg
l
U
Uq
ma x = q ⇒ a x =
d
md
Uqt k2
x(t k ) = d =
⇒ tk =
2md
X
F
E
d
2md 2
Uq
gt k2 gmd 2
=
⇒
Uq
2
U
Y
l
(…)
… grawitacji, która jest
zawsze równoległa do siły dośrodkowej, należy
rozwiązać następujące równanie.
mV 2
+ mg = qVB
R
⇒
m=
qVB
V2
+g
R
V1
X
17.7.R.
mV 2
mV 2
2E
mV
2mE
⇒V =
= qVB ⇒ R =
=
m
R
2
qB
qB
1
2πR 2πmV 2πm
qB
=
=
⇒
f =
T=
f =
T
V
qBV
qB
2πm
E=
W przypadku gdy V<<C (mechanika klasyczna) częstotliwość obiegu ładunku po
okręgu nie zależy od prędkości, a więc nie zależy od energii kinetycznej…
... zobacz całą notatkę






Komentarze użytkowników (0)