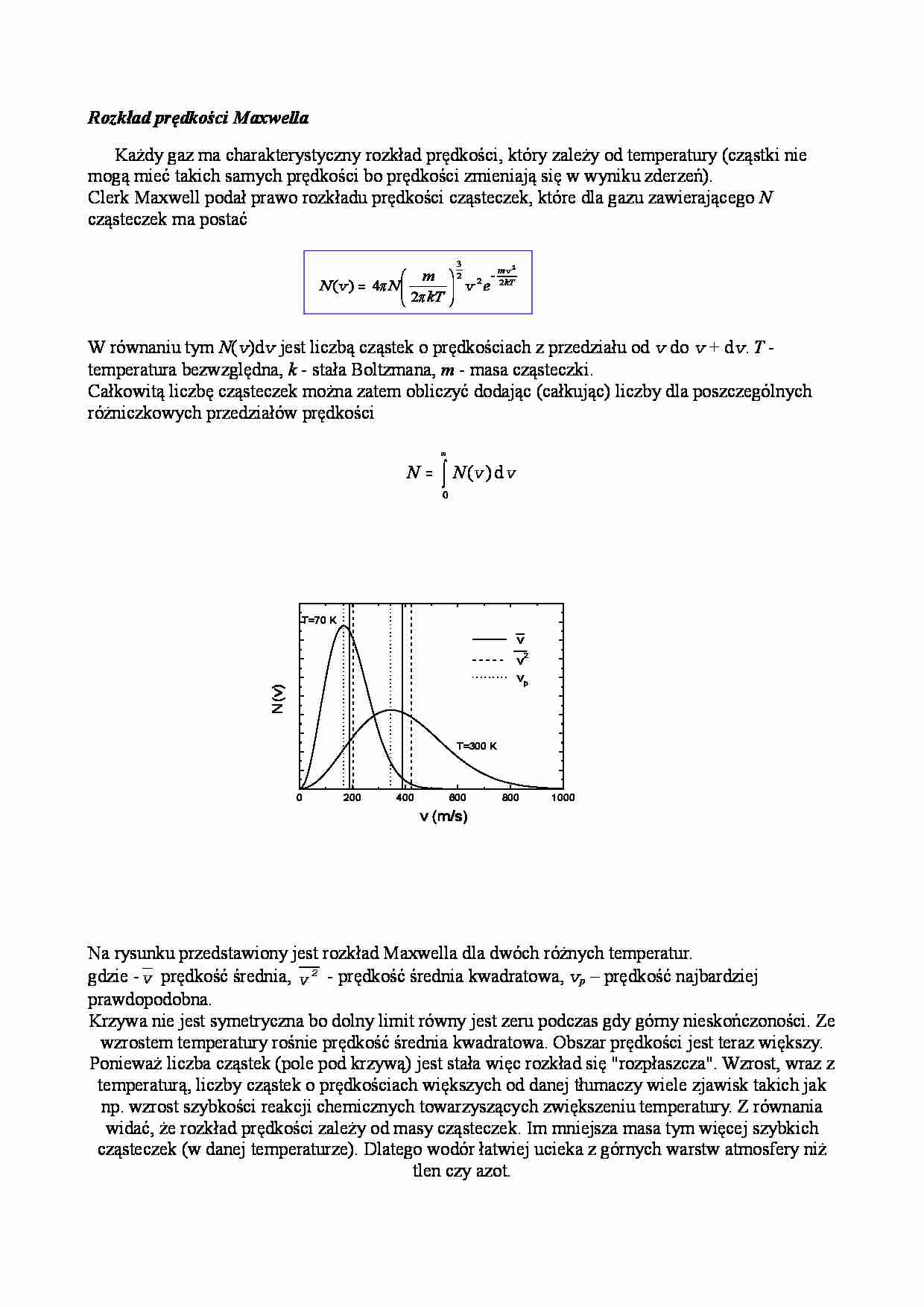
Rozkład prędkości Maxwella

Rozkład prędkości Maxwella Każdy gaz ma charakterystyczny rozkład prędkości, który zależy od temperatury (cząstki nie  mogą mieć takich samych prędkości bo prędkości zmieniają się w wyniku zderzeń). Clerk Maxwell podał prawo rozkładu prędkości cząsteczek, które dla gazu zawierającego  N  cząsteczek ma postać kT m e kT m N N 2 2 2 3 2 2 4 ) ( v v v −       = π π W równaniu tym  N ( v )d v  jest liczbą cząstek o prędkościach z przedziału od  v  do  v  + d v .  T  -  temperatura bezwzględna,  k  - stała Boltzmana,  m  - masa cząsteczki. Całkowitą liczbę cząsteczek można zatem obliczyć dodając (całkując) liczby dla poszczególnych  różniczkowych przedziałów prędkości ∫ ∞ = 0 d ) ( v v N N Na rysunku przedstawiony jest rozkład Maxwella dla dwóch różnych temperatur. gdzie - v   prędkość średnia,   2 v   - prędkość średnia kwadratowa,  vp  – prędkość najbardziej  prawdopodobna. Krzywa nie jest symetryczna bo dolny limit równy jest zeru podczas gdy górny nieskończoności. Ze  wzrostem temperatury rośnie prędkość średnia kwadratowa. Obszar prędkości jest teraz większy.  Ponieważ liczba cząstek (pole pod krzywą) jest stała więc rozkład się "rozpłaszcza". Wzrost, wraz z  temperaturą, liczby cząstek o prędkościach większych od danej tłumaczy wiele zjawisk takich jak  np. wzrost szybkości reakcji chemicznych towarzyszących zwiększeniu temperatury. Z równania  widać, że rozkład prędkości zależy od masy cząsteczek. Im mniejsza masa tym więcej szybkich  cząsteczek (w danej temperaturze). Dlatego wodór łatwiej ucieka z górnych warstw atmosfery niż  tlen czy azot. 0 200 400 600 800 1000 __ _    v    v 2    v p v (m/s) N (v ) T=300 K T=70 K Document Outline Rozkład prędkości Maxwella ... zobacz całą notatkę