To tylko jedna z 11 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Prof. Teresa Kamińska
Równowaga cząstkowa (rynkowa) i ogólna
4. RÓWNOWAGA RYNKOWA (CZĘŚCIOWA) I OGÓLNA
W teorii ekonomii rozróżnia się modele równowagi nawiązujące do trzech definicji1:
1.
walrasowska – równowaga ogólna oznacza gospodarkę w „stanie spoczynku”, tj.
bezczasowo wyraża się w wielkości i strukturze produkcji, czynników produkcji i
poziomie cen, w którym popyt na produkcję i czynniki produkcji jest równy ich
podaży. Nawiązuje do optimum Pareta, ponieważ nie występują tutaj podmioty
zainteresowane zmianą tego stanu. Istnieje również całkowite podporządkowanie
mechanizmowi rynkowemu z wykluczeniem ingerencji zewnętrznej;
2.
neumannowska – gospodarka znajduje się w równowadze, jeśli może
równomiernie (np. ze stałą stopą) zwiększać produkcję przy niezmienionej
strukturze, przy czym zostaje zachowana pełna zgodność wzrostu
technologicznego z ekonomicznym.
3.
neoklasyczna koncepcja równowagi w wieloczynnikowych modelach wzrostu,
pośrednia między walrasowską i neumannowską, zgodnie z którą gospodarka
znajduje się w równowadze, jeżeli umożliwia równomierny wzrost wszystkich
podstawowych wielkości ekonomicznych: czynników produkcji, produkcji (dochodu)
i konsumpcji.
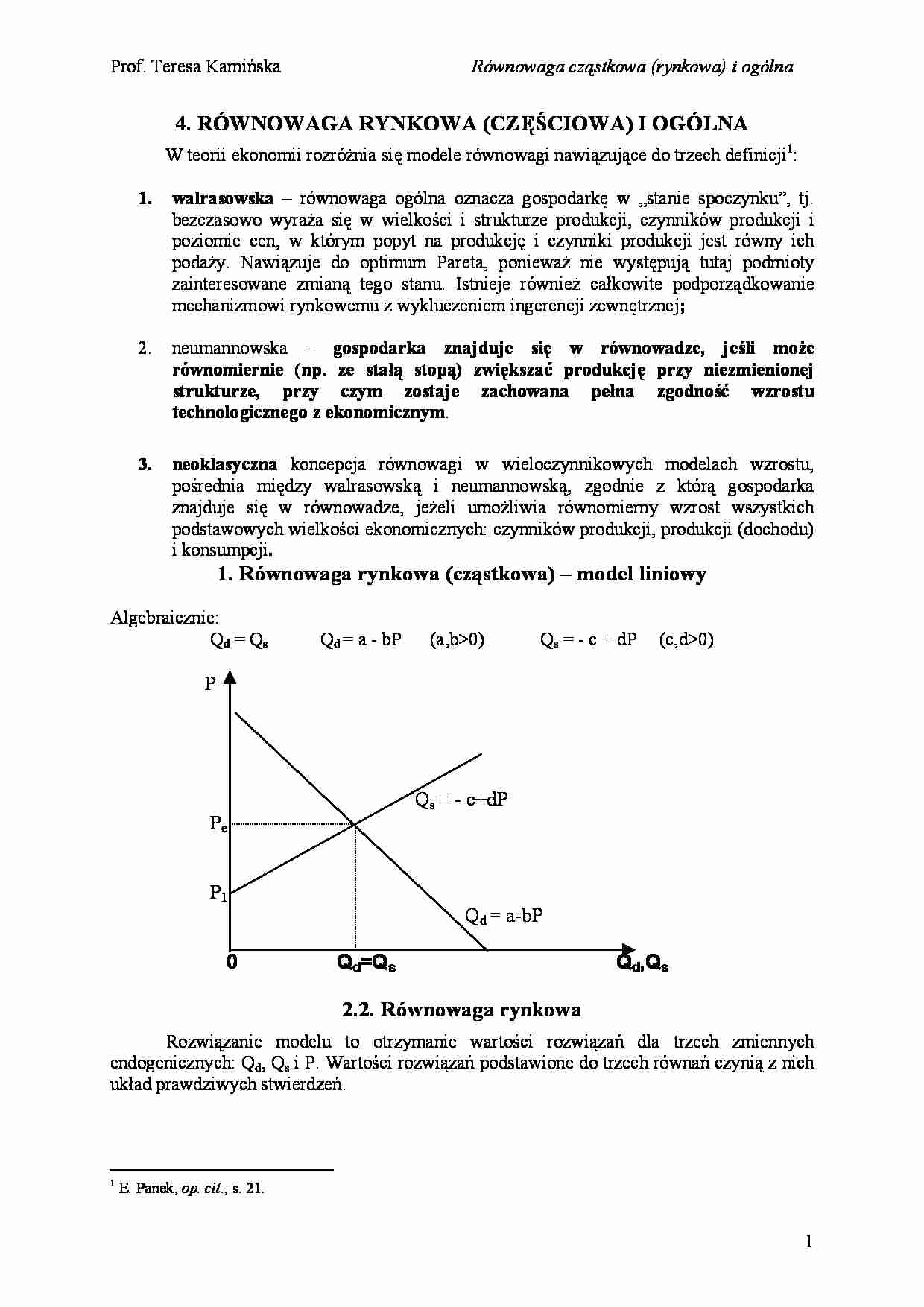
1. Równowaga rynkowa (cząstkowa) – model liniowy
Algebraicznie:
Qd = Qs
Qd = a - bP
(a,b0)
Qs = - c + dP
(c,d0)
P
Qs = - c+dP
Pe
P1
0
Qd = a-bP
Qd=Qs
Qd,Qs
2.2. Równowaga rynkowa
Rozwiązanie modelu to otrzymanie wartości rozwiązań dla trzech zmiennych
endogenicznych: Qd, Qs i P. Wartości rozwiązań podstawione do trzech równań czynią z nich
układ prawdziwych stwierdzeń.
1
E. Panek, op. cit., s. 21.
1
Prof. Teresa Kamińska
Pe =
a+c
b+d
Równowaga cząstkowa (rynkowa) i ogólna
Qe = a −
b(a + c) a (b + d ) − b(a + c) ad − bc
=
=
b+d
b+d
b+d
Ponieważ (b+d) jest dodatni, więc aby Q było dodatnie, licznik (ad-bc) również musi być
dodatni. Model ma sens ekonomiczny, gdy zawiera dodatkowy warunek adbc.
Jeżeli zbiór punktów na krzywych popytu i podaży oznaczy się odpowiednio D i S,
wtedy stosując symbol Q = Qd = Qs można zapisać dwa zbiory i ich przecięcie jako:
D={(P,Q|Q = a - bP}
D∩S = (Pe,Qe)
S={P,Q|Q = - c + dP}
Zbiór, który jest częścią wspólną, zawiera w tym wypadku tylko jeden element: parę
uporządkowaną (Pe,Qe). Równowaga rynkowa jest jedyna.
Edp Esp
S
P0
P2
Pe
1
2
3
4
5
t
P1
D
0
Q
Q1 Q3 Qe Q4 Q2 Q0
Gasnące oscylacje w modelu pajęczyny (rynek stabilny)
P
S
P0
Pe
t
1
2
3
P1
D
0
Q2
Qe
Q1
Q
Wybuchowe oscylacje (rynek niestabilny)
2
Prof. Teresa Kamińska
Równowaga cząstkowa (rynkowa) i ogólna
P
S
P0
Pe
t
P1
1
2
3
D
0
Q1 Qe
Q0
Q
Oscylacje jednostajne
Model rynku dwóch dóbr
Zakłada się, że funkcje popytu i podaży są liniowe.
Qd1 – Qs1 = 0
Qd1 = a0 + a1P1 + a2P2
Qs1 = b0 + b1P1 + b2P2
Qd2 – Qs2 = 0
Qd2 = α0 + α1P1 + α2P2
Qs2 = β0 + β1P1 + β2P2.
Eliminując zmienne, tj. podstawiając równanie drugie i trzecie do pierwszego oraz piąte i
szóste do czwartego, redukuje się model do dwu równań z dwiema zmiennymi:
(a0 – b0)
(…)
…
•
a21
01
02
x = (x1, x2)
•
a = (a1, a2)
a11
a22
a11 + a12
Ograniczenia wyboru obu dóbr wynoszą odpowiednio:
a11 + a12 i a21 + a22. Każdy punkt w prostokącie (np. a i x) odpowiada
pewnemu dopuszczalnemu podziałowi wszystkich dóbr na rynku.
7
Prof. Teresa Kamińska
x2
Równowaga cząstkowa (rynkowa) i ogólna
8. krzywe obojętności obu konsumentów, odpowiadające ich
preferencjom tworzą mapy silnie wypukłe
02…
... zobacz całą notatkę






Komentarze użytkowników (0)