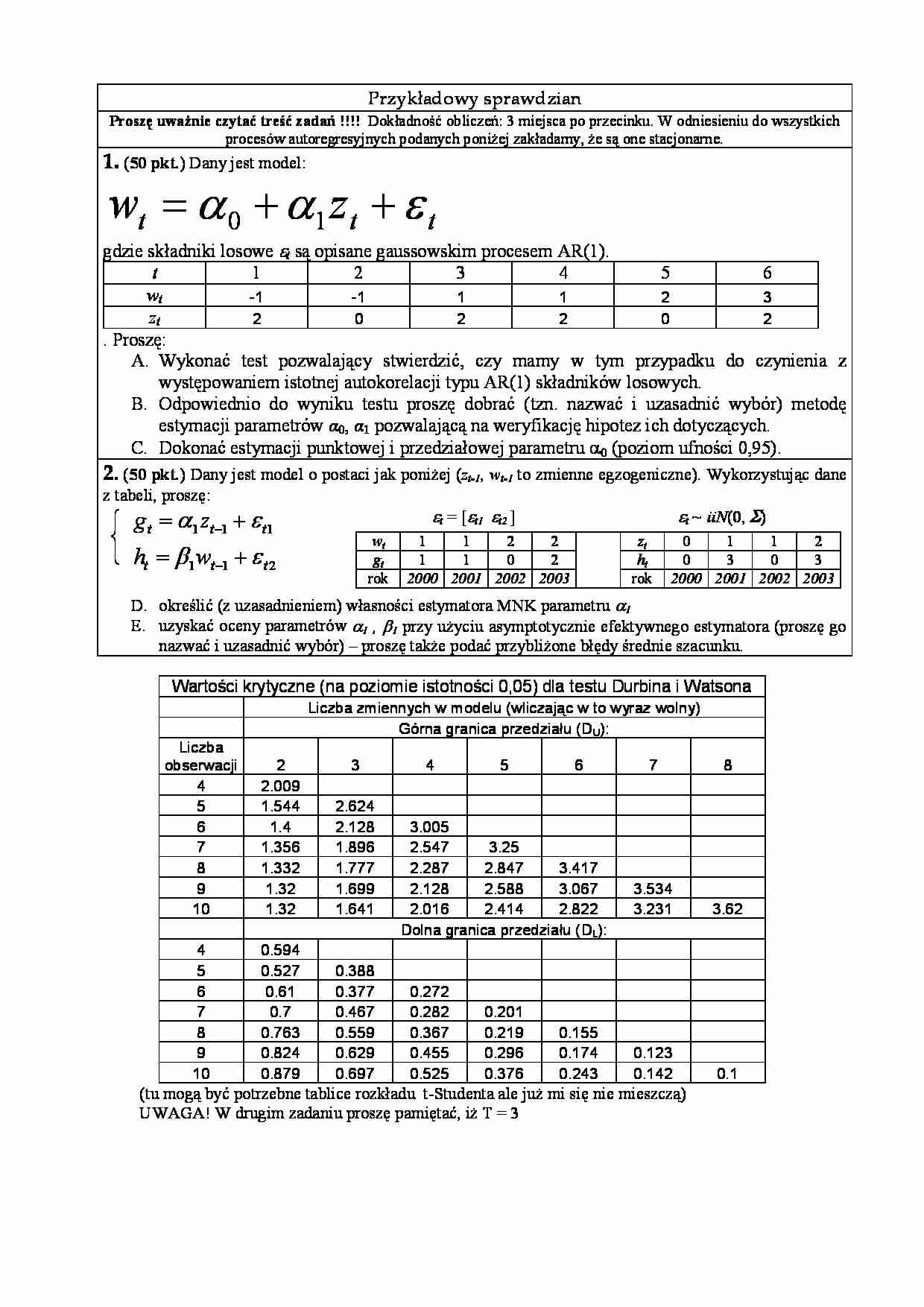
Przykładowy sprawdzian Proszę uważnie czytać treść zadań !!!! Dokładność obliczeń: 3 miejsca po przecinku. W odniesieniu do wszystkich procesów autoregresyjnych podanych poniżej zakładamy, że są one stacjonarne. 1. ( 50 pkt. ) Dany jest model: t t t z w ε α α + + = 1 0 gdzie składniki losowe ε t są opisane gaussowskim procesem AR(1). t 1 2 3 4 5 6 wt -1 -1 1 1 2 3 zt 2 0 2 2 0 2 . Proszę: A. Wykonać test pozwalający stwierdzić, czy mamy w tym przypadku do czynienia z występowaniem istotnej autokorelacji typu AR(1) składników losowych. B. Odpowiednio do wyniku testu proszę dobrać (tzn. nazwać i uzasadnić wybór) metodę estymacji parametrów α 0, α 1 pozwalającą na weryfikację hipotez ich dotyczących. C. Dokonać estymacji punktowej i przedziałowej parametru α0 (poziom ufności 0,95). 2. ( 50 pkt. ) Dany jest model o postaci jak poniżej ( zt-1 , wt-1 to zmienne egzogeniczne). Wykorzystując dane z tabeli, proszę: 2 1 1 1 1 1 t t t t t t w h z g ε β ε α + = + = − − ε t = [ε t1 ε t2 ] ε t ~ iiN ( 0 , Σ) wt 1 1 2 2 zt 0 1 1 2 gt 1 1 0 2 ht 0 3 0 3 rok 2000 2001 2002 2003 rok 2000 2001 2002 2003 D. określić (z uzasadnieniem) własności estymatora MNK parametru α 1 E. uzyskać oceny parametrów α 1 , β 1 przy użyciu asymptotycznie efektywnego estymatora (proszę go nazwać i uzasadnić wybór) – proszę także podać przybliżone błędy średnie szacunku. Wartości krytyczne (na poziomie istotności 0,05) dla testu Durbina i Watsona Liczba zmiennych w modelu (wliczając w to wyraz wolny) Górna granica przedziału (DU): Liczba obserwacji 2 3 4 5 6 7 8 4 2.009 5 1.544 2.624 6 1.4 2.128 3.005 7 1.356 1.896 2.547 3.25 8 1.332 1.777 2.287 2.847 3.417 9 1.32 1.699 2.128 2.588 3.067 3.534 10 1.32 1.641 2.016 2.414 2.822 3.231 3.62 Dolna granica przedziału (DL): 4 0.594 5 0.527 0.388 6 0.61 0.377 0.272 7 0.7 0.467 0.282 0.201
... zobacz całą notatkę



Komentarze użytkowników (0)