To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
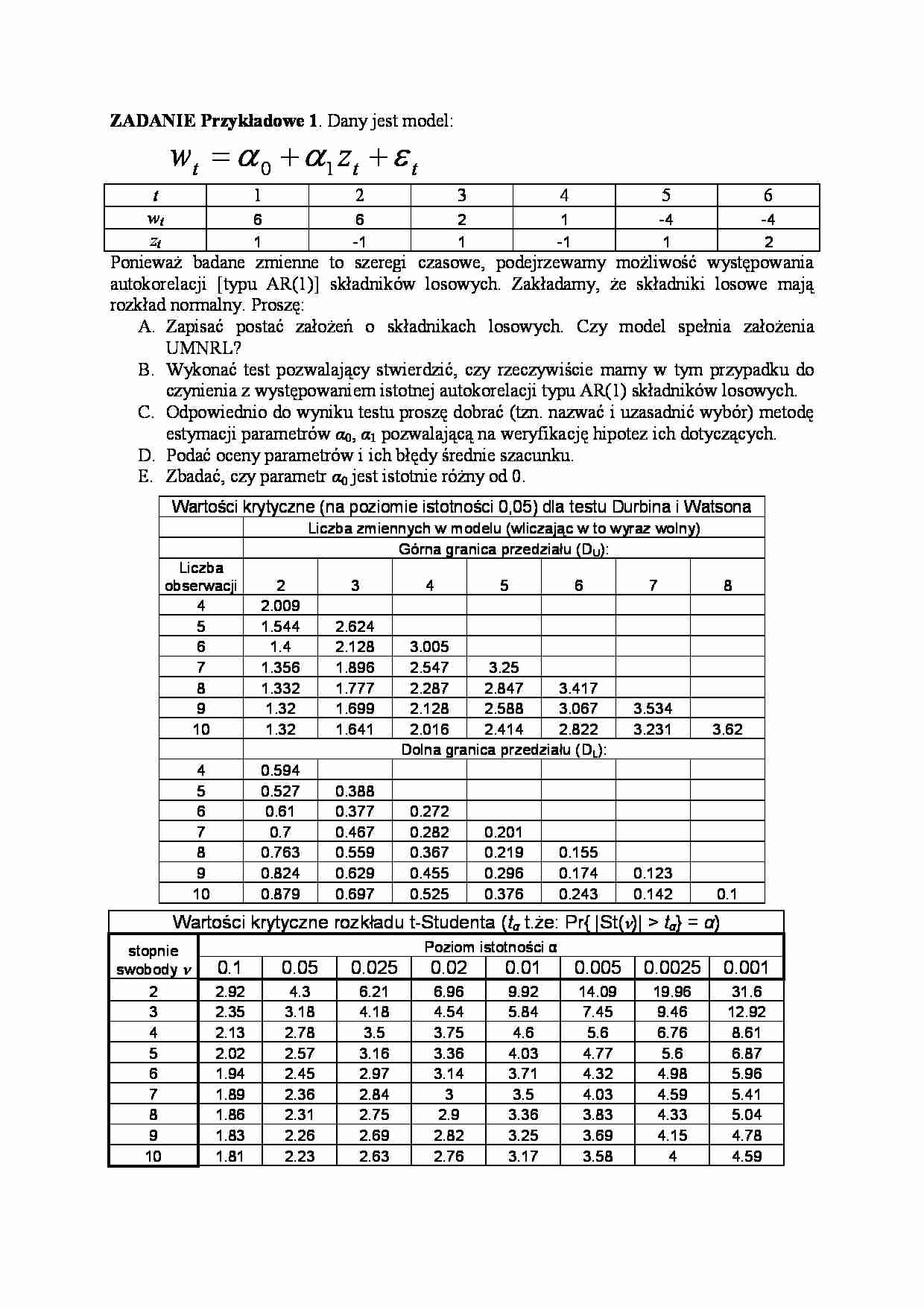

ZADANIE Przykładowe 1 . Dany jest model: t t t z w ε α α + + = 1 0 t 1 2 3 4 5 6 wt 6 6 2 1 -4 -4 zt 1 -1 1 -1 1 2 Ponieważ badane zmienne to szeregi czasowe, podejrzewamy możliwość występowania autokorelacji [typu AR(1)] składników losowych. Zakładamy, że składniki losowe mają rozkład normalny. Proszę: A. Zapisać postać założeń o składnikach losowych. Czy model spełnia założenia UMNRL? B. Wykonać test pozwalający stwierdzić, czy rzeczywiście mamy w tym przypadku do czynienia z występowaniem istotnej autokorelacji typu AR(1) składników losowych. C. Odpowiednio do wyniku testu proszę dobrać (tzn. nazwać i uzasadnić wybór) metodę estymacji parametrów α 0, α 1 pozwalającą na weryfikację hipotez ich dotyczących. D. Podać oceny parametrów i ich błędy średnie szacunku. E. Zbadać, czy parametr α 0 jest istotnie różny od 0. Wartości krytyczne (na poziomie istotności 0,05) dla testu Durbina i Watsona Liczba zmiennych w modelu (wliczając w to wyraz wolny) Górna granica przedziału (DU): Liczba obserwacji 2 3 4 5 6 7 8 4 2.009 5 1.544 2.624 6 1.4 2.128 3.005 7 1.356 1.896 2.547 3.25 8 1.332 1.777 2.287 2.847 3.417 9 1.32 1.699 2.128 2.588 3.067 3.534 10 1.32 1.641 2.016 2.414 2.822 3.231 3.62 Dolna granica przedziału (DL): 4 0.594 5 0.527 0.388 6 0.61 0.377 0.272 7 0.7 0.467 0.282 0.201 8 0.763 0.559 0.367 0.219 0.155 9 0.824 0.629 0.455 0.296 0.174 0.123 10 0.879 0.697 0.525 0.376 0.243 0.142 0.1 Wartości krytyczne rozkładu t-Studenta ( tα t.że: Pr{ |St(ν)| tα } = α ) stopnie swobody ν Poziom istotności α 0.1 0.05 0.025 0.02 0.01 0.005 0.0025 0.001 2 2.92 4.3 6.21 6.96 9.92 14.09 19.96 31.6 3 2.35 3.18 4.18 4.54 5.84 7.45 9.46 12.92 4 2.13 2.78 3.5 3.75 4.6 5.6 6.76 8.61 5 2.02 2.57 3.16 3.36 4.03 4.77 5.6 6.87 6 1.94 2.45 2.97 3.14 3.71 4.32 4.98 5.96
... zobacz całą notatkę




Komentarze użytkowników (0)