To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
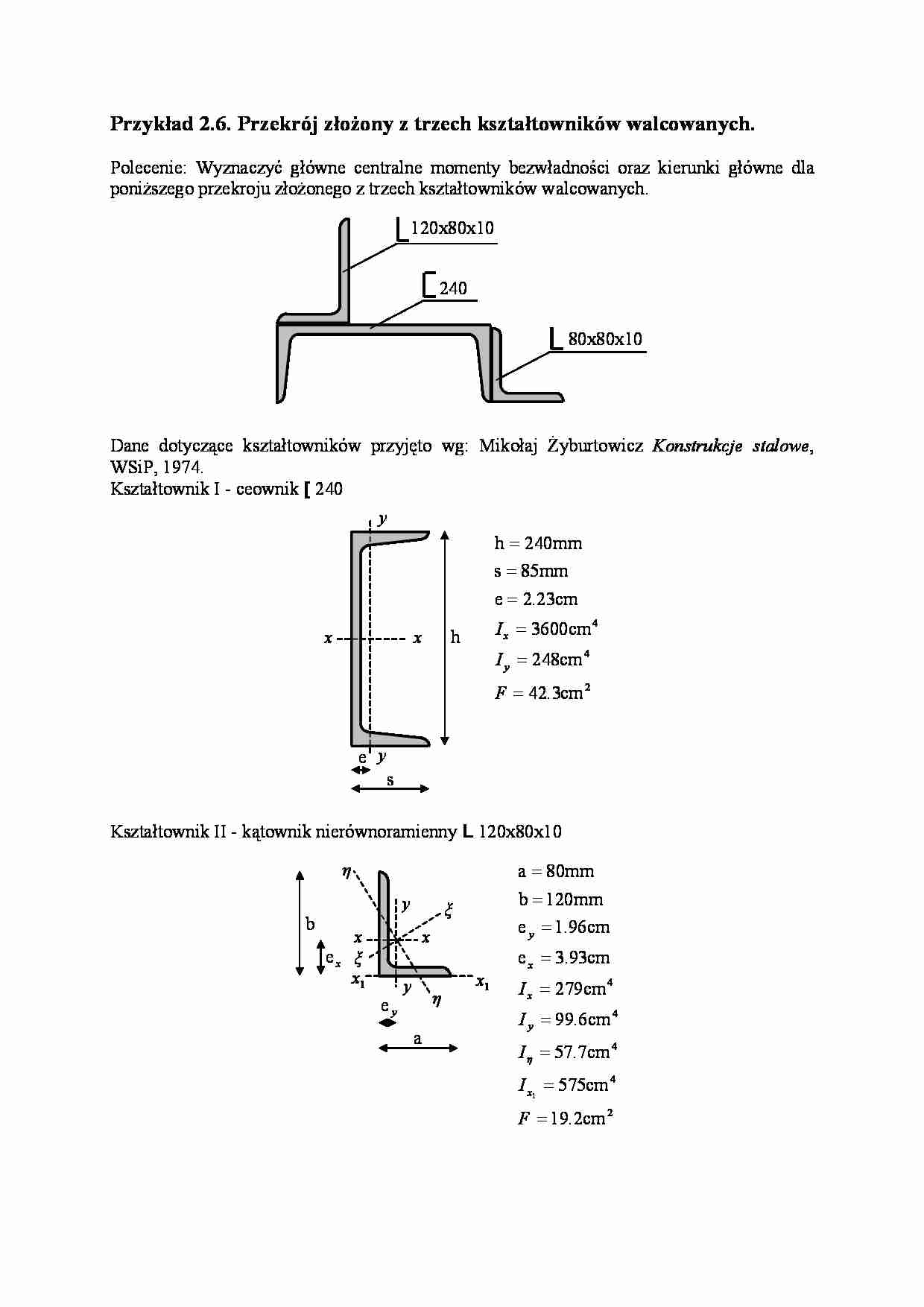


Przykład 2.6. Przekrój złożony z trzech kształtowników walcowanych.
Polecenie: Wyznaczyć główne centralne momenty bezwładności oraz kierunki główne dla
poniższego przekroju złożonego z trzech kształtowników walcowanych.
120x80x10
240
80x80x10
Dane dotyczące kształtowników przyjęto wg: Mikołaj Żyburtowicz Konstrukcje stalowe,
WSiP, 1974.
Kształtownik I - ceownik [ 240
y
h = 240mm
s = 85mm
e = 2.23cm
x
x
I x = 3600cm 4
h
I y = 248cm 4
F = 42.3cm 2
e y
s
Kształtownik II - kątownik nierównoramienny L 120x80x10
a = 80mm
b = 120mm
e y = 1.96cm
η
y
b
x
ex ξ
x1
ξ
x
ey
y
η
a
x1
e x = 3.93cm
I x = 279cm 4
I y = 99.6cm 4
I η = 57.7cm 4
I x1 = 575cm 4
F = 19.2cm 2
Kształtownik III - kątownik równoramienny L 80x80x10
η
ξ
y
a
e
x
ξ
a = 80mm
e = 2.35cm
x
I x = I y = 88.4cm 4
e y η
a
I ξ = 140cm 4
I η = 36.5cm 4
F = 15.1cm 2
W tablicach do projektowania konstrukcji stalowych nie są podane wartości
momentów dewiacyjnych, których znajomość jest nieodzowna do wyznaczenia głównych
centralnych momentów bezwładności oraz kierunków głównych dla rozpatrywanego
przekroju złożonego. Moment dewiacyjny ceownika względem jego osi centralnych jest
równy zero, gdyż oś x jest osią symetrii przekroju. Momenty dewiacyjne obu kątowników w
układzie xy są różne od zera. W celu wyznaczenia momentu dewiacyjnego skorzystamy ze
wzorów na główne momenty bezwładności:
I 1 = I max =
I 2 = I min =
Ix + Iy
2
Ix + Iy
2
2
⎛ Ix − Iy
+ ⎜
⎜ 2
⎝
⎞
⎟ + I xy 2
⎟
⎠
⎛ Ix − Iy
− ⎜
⎜ 2
⎝
⎞
⎟ + I xy 2 .
⎟
⎠
2
Po odjęciu stronami otrzymamy:
2
⎛ Ix − Iy ⎞
2
I1 − I 2 = 2 ⋅ ⎜
⎟
⎜ 2 ⎟ + I xy .
⎠
⎝
Następnie po przekształceniu wzór na moment dewiacyjny przyjmie postać:
2
2
2
⎞
⎟ .
⎟
⎠
⎛ I − I2 ⎞ ⎛ Ix − I y ⎞
⎟ .
I xy = ± ⎜ 1
⎟ −⎜
⎟
⎜
⎝ 2 ⎠ ⎝ 2 ⎠
W tablicach do projektowania konstrukcji stalowych kierunek maksymalnego
momentu bezwładności oznaczony jest przez ξ, natomiast kierunek minimalnego momentu
bezwładności oznaczony jest przez η. Uwzględniając to otrzymamy wzór:
⎛ Iξ − Iη ⎞ ⎛ I x − I y
I xy = ± ⎜
⎟ ⎜
⎜ 2 ⎟ −⎜ 2
⎠ ⎝
⎝
Wyznaczamy momenty dewiacyjne dla kątowników.
2
Kształtownik II - kątownik nierównoramienny L 120x80x10
W tablicach do projektowania konstrukcji stalowych podana jest tylko wartość
minimalnego momentu bezwładności I η . W celu wyznaczenia wartości I ξ skorzystamy z
zależności
I x + I y = Iξ + Iη ,
czyli
Iξ = I x + I y − Iη .
2
Po podstawieniu wartości odczytanych z tablic otrzymamy
I ξ = I x + I y − I η = 279cm 4 + 99.6cm 4 − 57.7cm 4 = 320.9cm 4
Wyznaczamy moment dewiacyjny
I xy
⎛ Iξ − Iη
=± ⎜
⎜ 2
⎝
2
⎞ ⎛ Ix − Iy
⎟ −⎜
⎟ ⎜ 2
⎠ ⎝
2
⎞
⎟ =±
⎟
⎠
⎛ 320.9cm 4 − 57.7cm 4
⎜
⎜
2
⎝
2
⎞ ⎛ 279cm 4 − 99.6cm 4
⎟ −⎜
⎟ ⎜
2
⎠ ⎝
2
⎞
⎟ =
⎟
⎠
= ±96.29cm 4
Znak momentu dewiacyjnego zależy od położenia kątownika nierównoramiennego w
stosunku do układu osi centralnych xy.
y
x
C
W rozpatrywanym przypadku w pierwszej i trzeciej ćwiartce układu współrzędnych, w
których iloczyn współrzędnych x·y jest dodatni, znajduje się większa część pola figury (na
(…)
… c1
xc 2
C2
I
O
xc1
C1
12cm
yc3
x
C3 xc 3
12cm
8cm 0.5cm
y
yc 2
8.5cm
12cm
8cm
8cm
III
W celu wyznaczenia współrzędnych środka ciężkości figury złożonej określamy pola
powierzchni i współrzędne środków ciężkości w układzie Oxy dla figur składowych na
podstawie tablic do projektowania konstrukcji stalowych.
~ =0
~ = −2.23cm
A I = 42.3cm 2
xc1
y c1
II
2
~ = −(4 + 1.96)cm = −5.96cm
~ = 3.93cm
A = 19.2cm…
... zobacz całą notatkę






Komentarze użytkowników (0)