To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
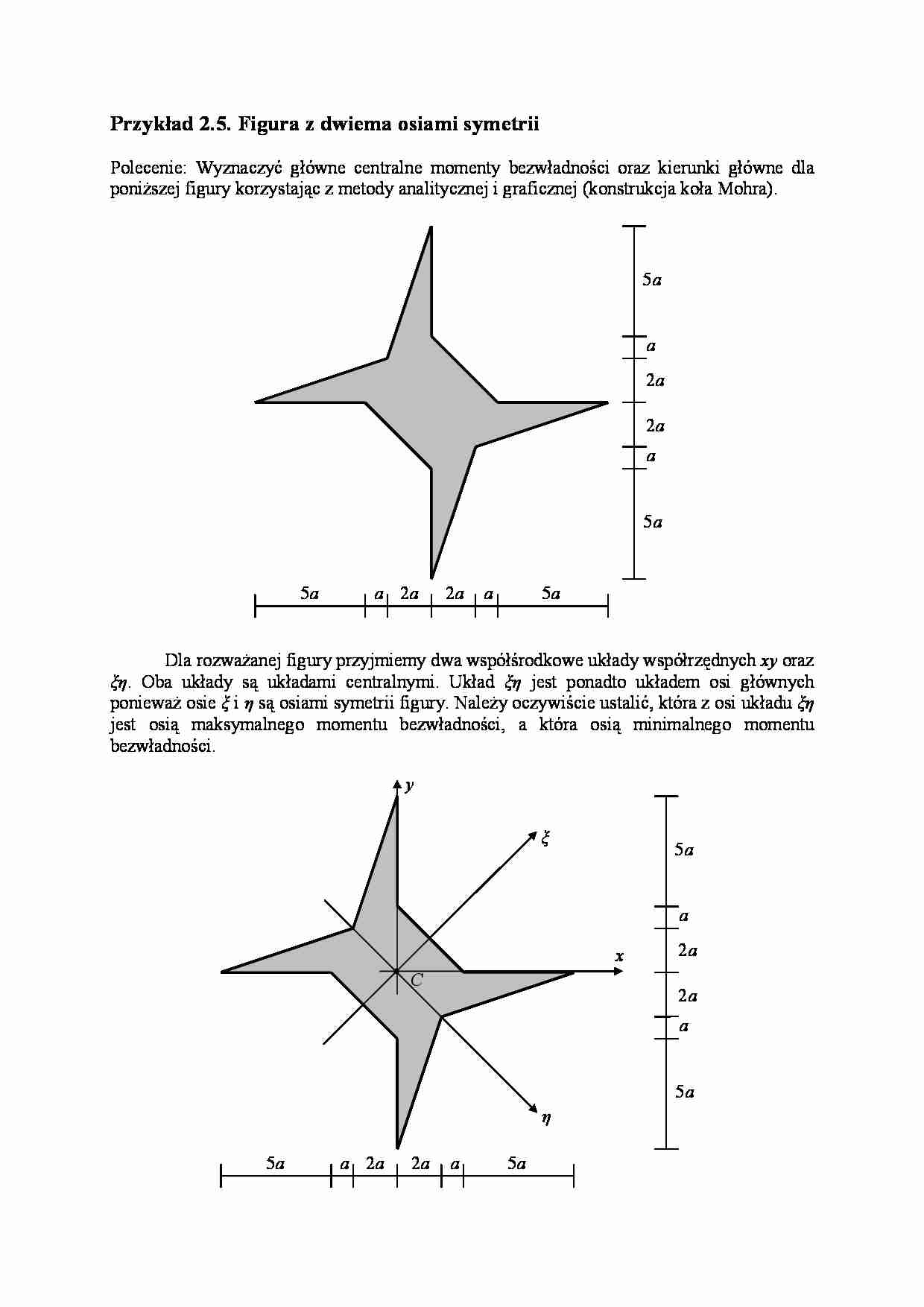


Przykład 2.5. Figura z dwiema osiami symetrii
Polecenie: Wyznaczyć główne centralne momenty bezwładności oraz kierunki główne dla
poniższej figury korzystając z metody analitycznej i graficznej (konstrukcja koła Mohra).
5a
a
2a
2a
a
5a
5a
a 2a
2a
a
5a
Dla rozważanej figury przyjmiemy dwa współśrodkowe układy współrzędnych xy oraz
ξη. Oba układy są układami centralnymi. Układ ξη jest ponadto układem osi głównych
ponieważ osie ξ i η są osiami symetrii figury. Należy oczywiście ustalić, która z osi układu ξη
jest osią maksymalnego momentu bezwładności, a która osią minimalnego momentu
bezwładności.
y
ξ
5a
a
x
C
2a
2a
a
5a
η
5a
a 2a
2a
a
5a
W celu wyznaczenia momentu bezwładności względem osi x dokonamy podziału
rozpatrywanej figury na figury składowe.
y
yc 4
5a
yc4
xc 4
C4
IV
III C3
xc4
II
a
C
x
I
2a
2a
a
5a
5a
a 2a
2a
a
5a
Moment bezwładności rozpatrywanej figury względem osi x policzymy jako
podwojoną sumę momentów bezwładności względem osi x figur składowych (figury I, II, III i
IV). Moment bezwładności figury względem osi y ma taką samą wartość. W przypadku figury
IV należy zastosować twierdzenie Steinera. Pole powierzchni figury III i IV wynosi
1
A III = A IV = ⋅ 2a ⋅ 6a = 6a 2
2
I
II
III
IV
Ix = Iy = 2⋅ Ix + Ix + Ix + Ix =
(
)
2
⎧1
⎡1
1
1
1
⎪
⎪
⎞ ⎤⎫
3
3
3
3
2 ⎛
= 2 ⋅ ⎨ ⋅ 3a ⋅ (3a ) + ⋅ 2a ⋅ (2a ) + ⋅ 6a ⋅ (2a ) + ⎢ ⋅ 2a ⋅ (6a ) + 6a ⋅ ⎜ 2a + ⋅ 6a ⎟ ⎥ ⎬ =
3
12
3
⎝
⎠ ⎥⎪
⎪12
⎢ 36
⎣
⎦⎭
⎩
1
= 248 a 4
6
Dewiacyjny moment rozpatrywanej figury w układzie xy policzymy jako podwojoną
sumę momentów dewiacyjnych figur składowych (figury I, II, III i IV). W przypadku figury
III i IV należy zastosować twierdzenie Steinera. Momenty dewiacyjne tych dwóch figur w
układzie xy mają te same wartości, można więc w obliczeniach uwzględnić to, licząc
podwojoną wartość momentu dewiacyjnego np. dla figury III.
I
II
III
IV
I
II
III
I xy = 2 ⋅ I xy + I xy + I xy + I xy = 2 ⋅ I xy + I xy + 2 ⋅ I xy =
(
)
(
)
⎧1
⎡1
1
1
⎛ 1
⎞ ⎛
⎞⎤ ⎫
2
2
2
2
2
2
= 2 ⋅ ⎨ (3a ) ⋅ (3a ) − (2a ) ⋅ (2a ) + 2 ⋅ ⎢ (2a ) ⋅ (6a ) + 6a 2 ⋅ ⎜ − ⋅ 2a ⎟ ⋅ ⎜ 2a + ⋅ 6a ⎟⎥ ⎬ =
4
3
⎝ 3
⎠ ⎝
⎠⎦ ⎭
⎣ 72
⎩ 24
1
= −57 a 4
4
Główna oś bezwładności, względem której moment bezwładności ma wartość
2
I 1 = I max tworzy z osią x kąt ϕ1 , natomiast główna oś bezwładności, względem której
moment bezwładności ma wartość I 2 = I min tworzy z osią x kąt ϕ 2 .
π
π
Ponieważ Ix = Iy , Ixy
... zobacz całą notatkę






Komentarze użytkowników (0)