To tylko jedna z 57 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
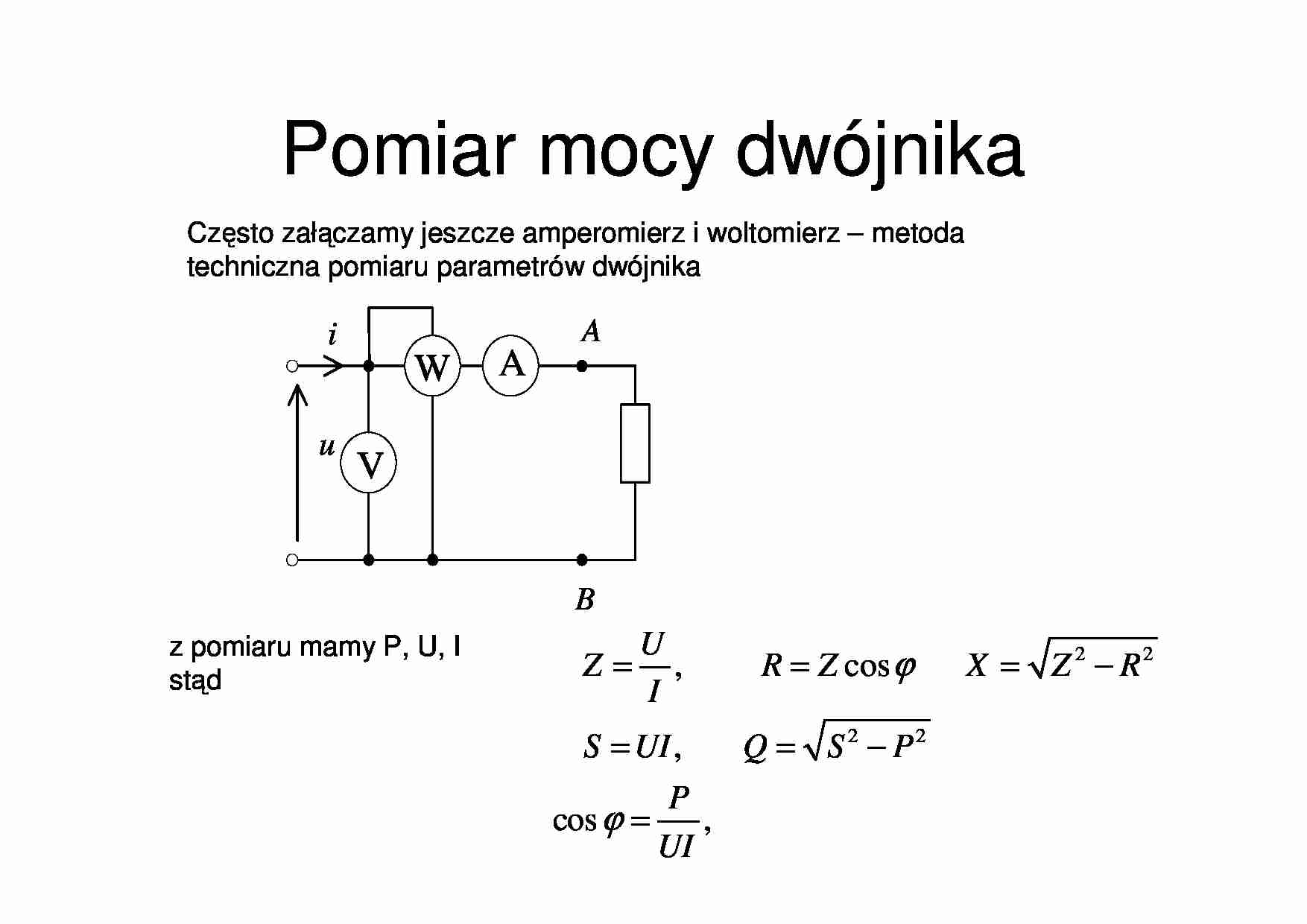

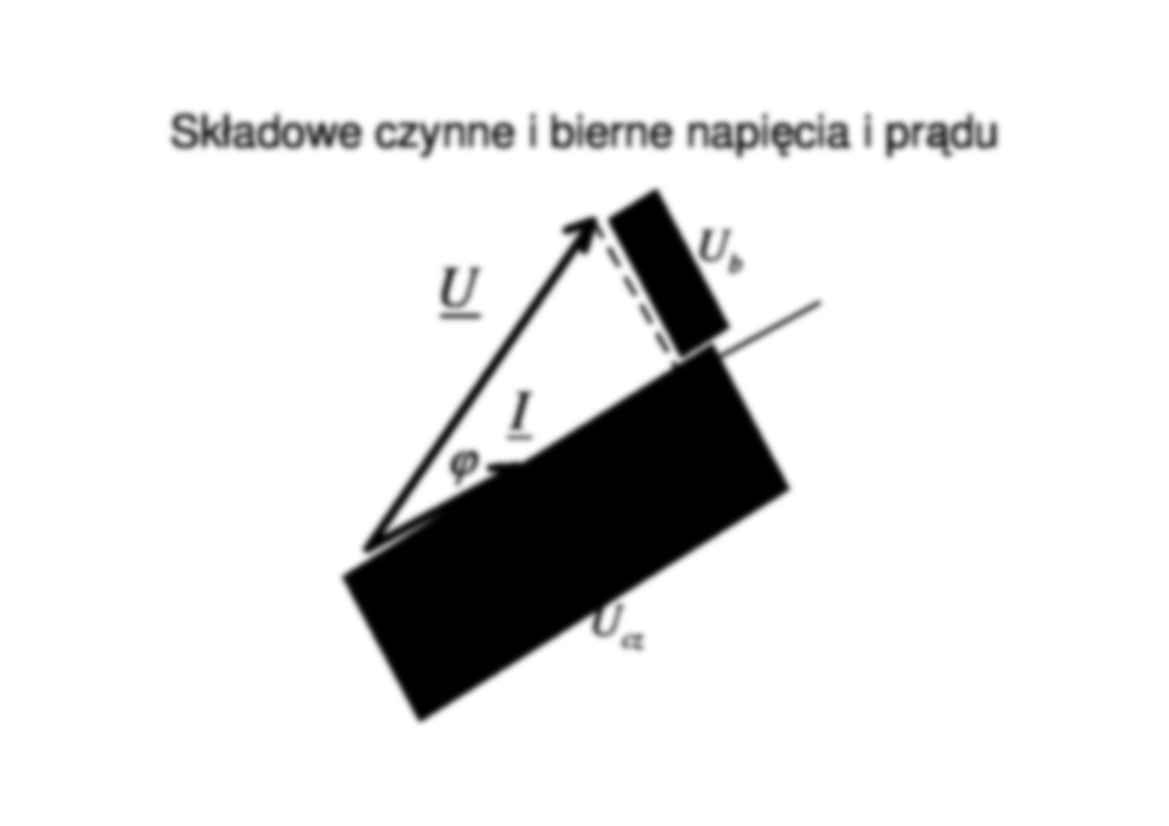
Pomiar mocy dwójnika W u i A B A V 2 2 2 2 , cos , cos , U Z R Z X Z R I S UI Q S P P UI ϕ ϕ = = = − = = − = Często załączamy jeszcze amperomierz i woltomierz – metoda techniczna pomiaru parametrów dwójnika z pomiaru mamy P, U, I stąd Składowe czynne i bierne napięcia i prądu cos ; cos ; sin ; sin ; cz cz cz b b b P P UI IU U U U RI I Q Q UI IU U U U XI I ϕ ϕ ϕ ϕ = = = = = = = = = = { } Re cz U U ≠ U cz; Ub – składowe czynne i bierne napięcia Składowa czynna – rzut wskazu napięcia na kierunek wyznaczony przez wskaz prądu. Składowa bierna – rzut wskazu napięcia na kierunek prostopadły do kierunku wyznaczonego przez wskaz prądu. Ogólnie Składowe czynne i bierne napięcia i prądu cz U b U U I ϕ Składowe czynne i bierne napięcia i prądu cz U 0 b U U I ϕ 0 ϕ cz U 0 b U cos ; ; sin ; cz cz cz b b b P I I I I GU U Q I I I I BU U ϕ ϕ = = = − = − = = Analogicznie dla prądu Składowe czynne i bierne napięcia i prądu C X C R I b I cz I ϕ δ I U cz I b I 2 2 1 cos cos sin sin C cz b cz C R b C C I YU I I I I UY UG U I R I I UY UB U C I ϕ ϕ ϕ ϕ ω = = + = = = = = = = = = = b C cz I R C I ω = 1 cz R b C C I I tg I I R C δ ω = = = np. rzeczywisty kondensator Dobroć kondensatora współczynnik stratności Składowe czynne i bierne napięcia i prądu I 1 I 2 I 3 I 1 cos ϕ 2 cos ϕ 3 cos ϕ 1 I 2 I 3 I U 1 ϕ 2 ϕ 3 ϕ ( ) ( ) 2 2 2 2 1 1 2 2 3 3 1 1 2 2 3 3 2 2 cos cos cos sin sin sin cos sin cz b k k k k k k I I I I I I I I I I I ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ = + = + + + + + =
(…)
…
I
−ϕ
UC
U
Re
Odbiornik RLC
I
Zw
Im
R
UR
U
E
UC
UL
UL
UC
U
XC
UR
ϕ
I
NPK ⇒ U − U R − U L − U C = 0 ⇒ U = U R + U L + U C =
IR + I ( jX L − jX C ) = I ( R + jX L − jX C ) = I ( R + j ( X L − X C ) ) =
= I Z odb
Spadek napięcia i strata mocy w linii
Rl
Xl
Ul
U1
U 1 = U 2 + U l = U 2 + I ( Rl + jX l )
U1
I ( jX l )
Ul
U2
I
odb
U2
IR
spadek napięcia linii
∆U = U1 − U 2
U1
I ( jXl )
Ul
U2
ϕ
IR
2
I
∆U
∆U = U1 − U 2 =
(U 2 cos ϕ2 + Rl I ) + (U 2 sin ϕ 2 + X l I )
2
2
−U2
spadek napięcia linii
C
U1
A
Ul
U2
I
strata napięcia
I ( jX l )
B
IR
∆U str = U 1 − U 2 = I ( Rl + jX l )
strata podłuŜna ( AB ) = RlIcosφ2 + XlIsinφ2
strata poprzeczna( BC ) =- RlIsinφ2 + XlIcosφ2
spadek napięcia linii
U1
C
ϕ
A
ϕ
U2
w przybliŜeniu spadek napięcia
∆U ≈ Rl I cos ϕ2 + X l I sin ϕ 2 = ( Rl I cos ϕ2 + X l I sin ϕ2…
… jak dla przebiegów chwilowych
∑ u j i j → ∑U j (t ) I j (t ) → ∑U j I j =
*
j
j
j
*
I1
.
T
I * = [U ]T I * = [ A]T [V ] [ I ]* =
U 1 ,..U j ,...U n ⋅ j
.
*
I n
= [V ] [ A][ I ] = [V ] [ A][ I ] = [V ] [ 0] = 0
T
czyli
*
*
T
n
∑S
j =1
j
T
=0
bilans mocy pozornej zespolonej.
Obwody elektryczne
Stąd z algebry liczb zespolonych
n
∑P
j =1
j
=0
bilans mocy czynnej…
…
n
∑Q
j =1
j
=0
bilans mocy biernej.
Zastosowanie bilansu mocy
Q j = Pj tgϕ j
Obliczyć prąd zasilający
P4
cosϕ4
A
U
P
1
cosϕ1
P2
cosϕ2
P
3
S
I= =
U
P2 + Q2 1
=
U
U
(∑ P ) + (∑ Q )
2
j
2
j
cosϕ3
wypadkowy kąt przesunięcia fazowego φ
wypadkowy współczynnik mocy cosφ
Q
tgϕ = =
P
cos ϕ =
P
=
S
∑Q
∑P
j
j
∑P
(∑ P ) + (∑ Q )
j
2
j
j
2
Metody obliczania obwodów
Metoda prądów oczkowych ( prądów konturowych…
... zobacz całą notatkę






Komentarze użytkowników (0)