To tylko jedna z 28 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


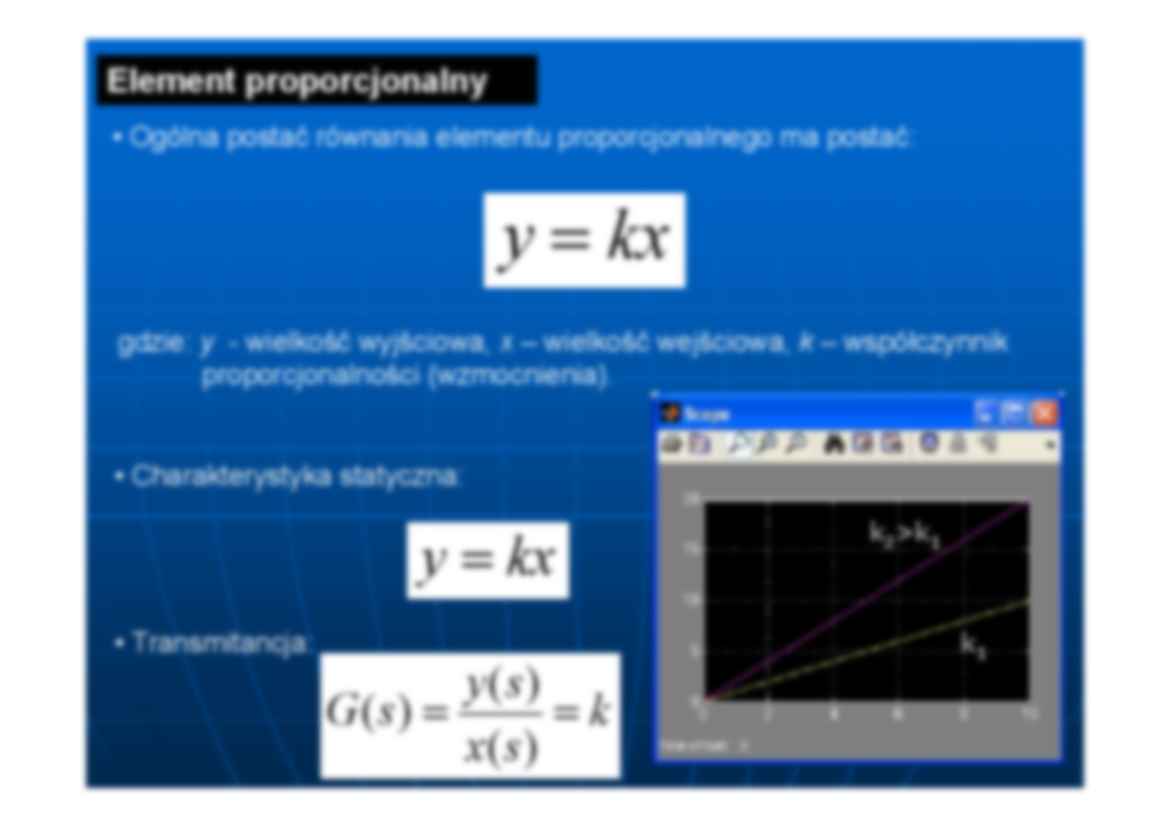
Wykład 4 • podstawowe elementy w automatyce Podstawowe elementy w automatyce • Podstawowe elementy układów automatyki można podzielić ze względu na ich właściwości dynamiczne na następujące grupy: - proporcjonalne, - inercyjne, - całkujące, - różniczkujące, - oscylacyjne, - opóźniające. • Dowolny element układu automatyki można scharakteryzować: - równaniem i wykresem charakterystyki statycznej, - równaniem różniczkowym i odpowiadającą mu transmitancją operato- rową - charakterystyką skokową. Element proporcjonalny • Ogólna postać równania elementu proporcjonalnego ma postać: kx y = gdzie: y - wielkość wyjściowa, x – wielkość wejściowa, k – współczynnik proporcjonalności (wzmocnienia). • Charakterystyka statyczna: • Transmitancja: kx y = k s x s y s G = = ) ( ) ( ) ( k 1 k 2k1 • Charakterystyka skokowa: ) ( 1 ) ( t t h = h(t) y(t)=kh(t) Element proporcjonalny (przykład) • Dzielnik napięcia Schemat: x=U 1 y=U 2 R 1 R 2 • dla dzielnika nap. obowiązuje następu – jąca zależność: 2 1 2 1 2 2 1 2 2 1 2 1 2 2 2 2 1 1 ) ( ) ( ) ( ) ( ) ( : postać ma a operatorow ncja transmita a : a nastepujac jest statyczna styka charaktery zatem stad R R R s x s y s U s U s G x R R R y R R R U U x y R U R R U + = = = + = + = = = + Przykłady innych elementów proporcjonalnych Element inercyjny pierwszego rzędu • Ogólna postać równania różniczkowego elementu inercyjnego pierwszego rzędu ma postać: kx y dt dy T = + skąd wynika transmitancja operatorowa: gdzie: k – współczynnik proporcjonalności (wzmocnienia), T – stała czasowa 1 ) ( ) ( ) ( + = = Ts k s x s y s G • Charakterystyka statyczna: kx y = • Charakterystyka skokowa (odpowiedź na wymuszenie skokowe x(t)=1(t)x st) : ) 1 ( ) ( ) 1 ( 1 ) ( 1 ) ( ) ( )] ( [ ) ( ) 1 ( 1 ) 1 ( ) ( 1 ) ( 1 T t st at st st st e kx t y e a a s s t f Oryginał s f ta Transforma s y L t y T s s x T k x Ts s k s y x s s x − − − − = − + = + = + = = M ) 1 ( ) ( T t st e kx t y − − = M. Żelazny, „Elementy automatyki” Element inercyjny pierwszego rzędu - przykłady u(t) i(t)
(…)
… obrotowy (sygn. wej.)
φ – współczynnik tarcia lepkiego
I – moment bezwładności
ω – prędkość kątowa (sygn. wyj.)
dω
M =I
+ ϕω
dt
1
I dω
+ω = M
ϕ dt
ϕ
1
I
T=
oraz k =
ϕ
y (t )
T
+ y (t ) = kx(t )
dt
ϕ
Schemat mechaniczny elementu inercyjnego I rzędu – sprężyna + tłumik.
x
K
D
y
B
Z rownowagi sił w punkcie D
dy
K ( x − y) = B
dt
B dy
+y=x
K dt
B
gdzie : = T ( stala czasowa )
K
Element całkujący
• Ogólna…
…
Dla sygn. jednoimiennych współczynnik
k ma wymiar odwrotności czasu:
dy
=x
T
dt
y(s) 1
=
G ( s) =
x( s ) Ts
gdzie: T – stała czasowa akcji całkującej,
stała całkowania
Element całkujący – zbiornik z wymuszonym poborem wody
Q2 ( P) nie zalezy od h
Q1
W stanie ustalonym :
A
Q10 = Q20
h
np. dla Q10 = const
Q2
P
Q1 i Q2
- objętościowe natężenia
przepływu (sygnały wej.)
h - poziom cieczy w zbiorniku
(sygnał wyj.)
otrzymamy charakterystyke
statyczna :
h0
hmax
0≤h0≤hmax
Q20=Q10
Q20
W stanie nieustalonym:
dh
A
= Q1 − Q2
dt
dh
= k (Q1 − Q2 )
dt
1
gdzie : k =
A
A − powierzchnia przekroju
poprzecznego zbiornika
h( s ) k
= ,
G1 ( s ) =
Q1 ( s ) s
h( s )
k
=−
G2 ( s ) =
Q2 ( s )
s
Q2 h
Q2st
Q2(t)
t
h(t)
Element całkujący – przekładnia cierna
x
Zakładamy brak poślizgu w punkcie
równowagi A:
2r
A
ω1=const
x…
... zobacz całą notatkę






Komentarze użytkowników (0)