WYKŁAD 27
DEFINICJA 27.1 (PARAMETRYZACJA REGULARNA)
Niech:
- obszar (zbiór otwarty i spójny)
ℑ : ∋ ℑ -parametryzacja regularna :⇔
1° 2° ℑ - ciągła i różniczkowalna w 3° ℑ - różnowartościowa (iniekcja)
4° W Każdym punkcie powierzchni Rℑ istnieje
wektor (A1,A2,A3) ⊥ Rℑ,
przy czym:
(A1,A2,A3) = Wyjaśnienie:
Rℑ - zbiór wartości odwzorowania ℑ (powierzchnia)
PRZYKŁAD 27.1
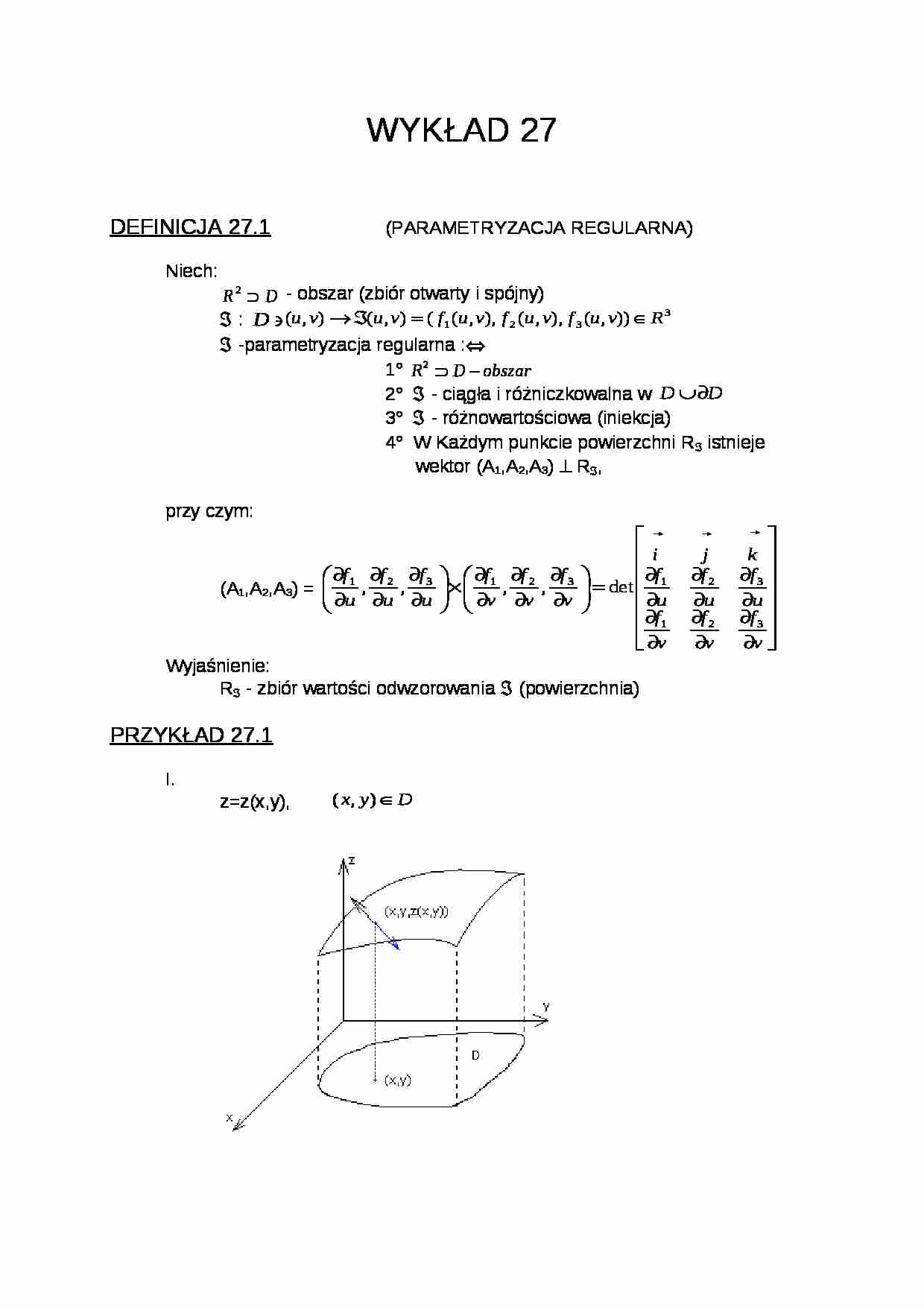
I. z=z(x,y), Niech:
ℑ : ∋ - parametryzacja naturalna
(A1,A2,A3) = ,czyli:
(A1,A2,A3) = II.
Gdy powierzchnia jest wykresem funkcji zmiennych x, z:
y=y(x,z), ℑ : ∋ Po analogicznym wyprowadzeniu jak w przypadku pierwszym: (A1,A2,A3) = III.
Gdy powierzchnia jest wykresem funkcji zmiennych y, z:
x=x(y,z), 1 ℑ : ∋ Więc:
(A1,A2,A3) = TWIERDZENIE 27.1
Z: ℑ : ∋ - parametryzacja
regularna
Niech:
κ : Δ ∋ κ - bijekcja, różniczkowalna
Niech:
G = ℑ κ : Δ ∋ G = Niech:
(B1,B2,B3) - wektor prostopadły do RG T: 1° Rℑ= RG 2° (B1,B2,B3) = (A1,A2,A3)∙Jκ ,gdzie:
Jκ = - jakobian odwzorowania κ D: Ad 1° ⇐ z założeń (bezpośrednio)
Ad 2° (B1,B2,B3) Dowód dla B2, B3 przeprowadza się analogicznie jak dla B1.
DEFINICJA 27.2 (PARAMETRYZACJE RÓWNOWAŻNE)
ℑ ∼ G ⇔ G= Jκ UWAGA:
1° Rℑ= RG 2° (A1,A2,A3) oraz (B1,B2,B3) mają ten sam kierunek, ten sam zwrot.
TWIERDZENIE 27.1
Relacja „∼” - jest relacją równowartościową.
(…)
…]⇔
⇔ -określona ciągła różniczkowalna (…) w .
DEFINICJA 27.6 (CAŁKA POWIERZCHNIOWA NIESKIEROWANA)
Niech -określona i ciągła na S=[ℑ]
PRZYKŁAD 27.2
Jeżeli S: z=z(x,y), WNIOSEK 27.1
1° Całka powierzchniowa niekierowana nie zależy od wyboru parametryzacji płata.
2° Całka powierzchniowa niekierowana nie zależy od orientacji płata.
DEFINICJA 27.7 (POWIERZCHNIA REGULARNA)
S - powierzchnia regularna ⇔ S -są płatami…
... zobacz całą notatkę





Komentarze użytkowników (0)