To tylko jedna z 11 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


W treści notatki z przedmiotu algebra liniowa znajduje się instruktaż jak odwracać macierze. Notatka pokazuje w kolejnych krokach na czym polega odwracanie macierzy. Przedstawiono dwie metody - za pomocą macierzy dopełnień algebraicznych i za pomocą oraz metodą operacji elementarnych. Wymieniono także założenia, które macierz musi spełnić żeby była odwracalna. Związane pojęcia: odwracanie macierzy, macierz nieosobliwa, metoda dopełnień algebraicznych, wyznacznik macierzy, macierze równoważne, macierz blokowa, rząd macierzy, minor, macierz bazowa, macierz kanoniczna. W notatce także przykładowe zadania do rozwiązania.
TECHNIKI ODWRACANIA MACIERZY
Elementarne wyznaczanie macierzy odwrotnej.
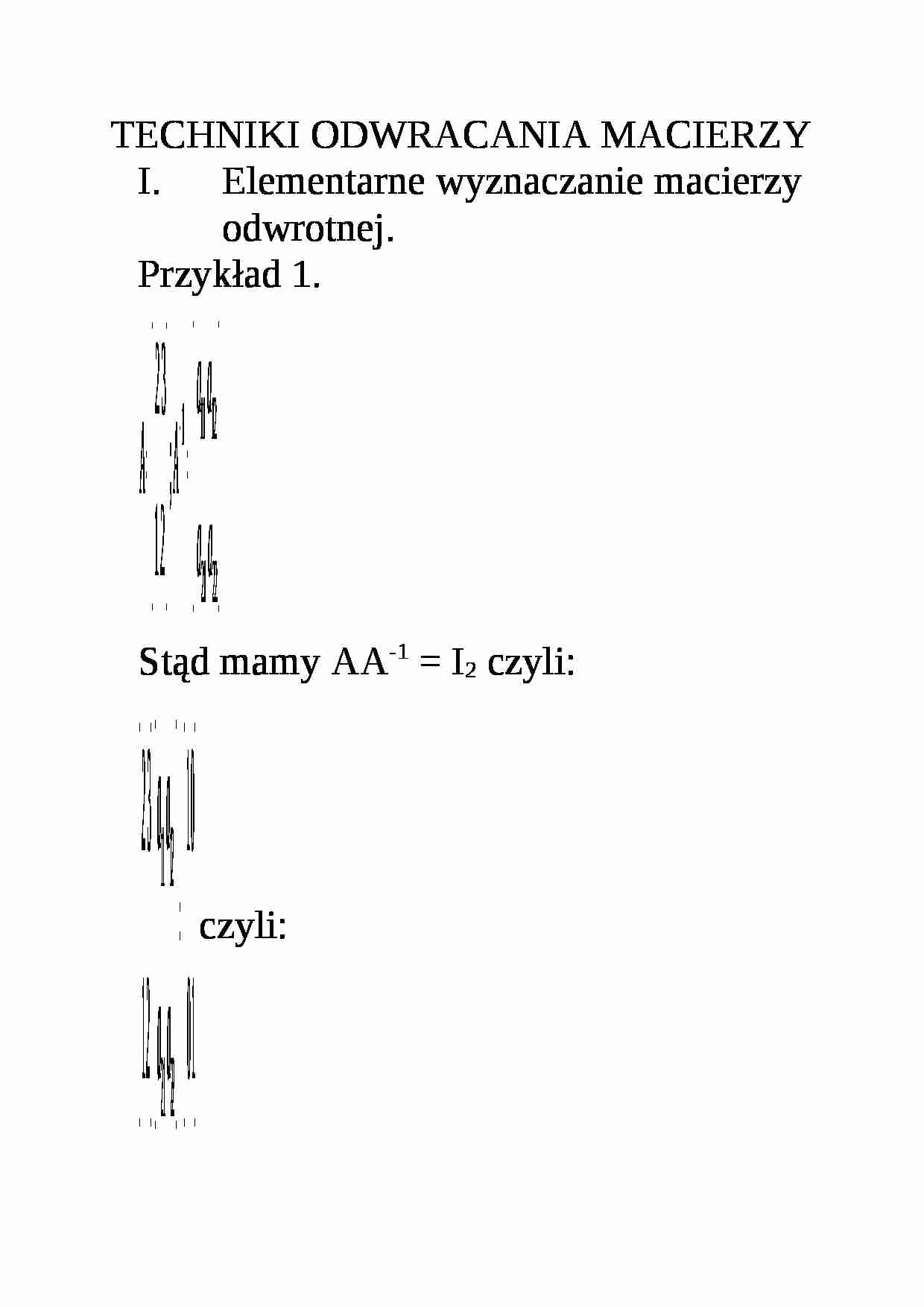
Przykład 1.
Stąd mamy AA-1 = I2 czyli:
czyli:
Stąd otrzymujemy układ czterech równań z czterema niewiadomymi, który daje się zapisać, ze względu na możliwość rozdzielenia zmiennych, jako dwa niezależne układy dwóch równań z dwiema niewiadomymi:
-
Skąd otrzymujemy:
a21=-1 ; a11=2 ; a22=2 ; a12=-3 . Czyli:
II. Metoda dopełnień algebraicznych.
Twierdzenie 1.
Jeżeli detA≠0 to
(A-1)-1=A
Twierdzenie 2.
Jeżeli macierze A i B są tego samego stopnia i są nieosobliwe, to:
(AB)-1=B-1A-1
Twierdzenie 3.
Jeżeli detA≠0 to
det(A-1)=(detA)-1
Twierdzenie 4.
Jeżeli detA≠0 i stA = n to:
A-1=(detA)-1DT ; (1)
gdzie D =[Dij]nxn oraz Dij=(-1)i+jMij
Przykład 2.
Wyznaczyć A-1 gdy:
Stąd stA=3 ; detA=-1≠0
Wyznaczymy macierz dopełnień D:
Stąd:
Zadanie 2 (domowe)
Wyznaczyć: detA; D; DT; A-1 dla macierzy A postaci:
Zadanie 3 (domowe)
Sprawdzić, czy prawdziwa jest równość:
X=A-1B, gdzie:
a) b) WYZNACZANIE MACIERZY ODWROTNEJ METODĄ OPERACJI ELEMENTARNYCH
Definicja Operacją elementarną na macierzy nazywamy:
przestawienie dwóch dowolnych wierszy (kolumn)
dodanie do wszystkich elementów dowolnego wiersza (kolumny) odpowiednio elementów innego wiersza (kolumny) pomnożonych przez dowolną liczbę
pomnożenie wszystkich elementów dowolnego wiersza (kolumny) przez dowolną liczbę różną od zera.
Definicja
Macierze A i B są równoważne, jeżeli A powstaje z B poprzez stosowanie operacji elementarnych. Fakt równoważności zapisujemy:
A ≈ B
Definicja
Macierz w której wyróżniono strukturę podmacierzy nazywamy blokową (jest złożona z bloków -macierzy prostokątnych).
Twierdzenie 5.
Niech stA=n. Jeżeli macierz blokowa C=[InD] powstała w wyniku operacji elementarnych na wierszach macierzy B=[AIn] to D=A-1
Przykład
Wyznaczyć macierz odwrotną do macierzy A, gdzie:
Dopisujemy do macierzy A blok macierzy I3 z prawej strony: Czyli mnożąc teraz macierz z prawej strony powy zszej równości przez 1/8 otrzymamy:
Wynik sprawdzamy mnożąc macierz A-1przez macierz A:
Zadanie domowe
Obliczyć macierz odwrotną do macierzy A:
Definicja
Rząd macierzy oznacza stopień maksymalnego niezerowego minora tej macierzy. Oznaczmy tę liczbę przez rgA.
... zobacz całą notatkę






Komentarze użytkowników (0)