To tylko jedna z 8 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
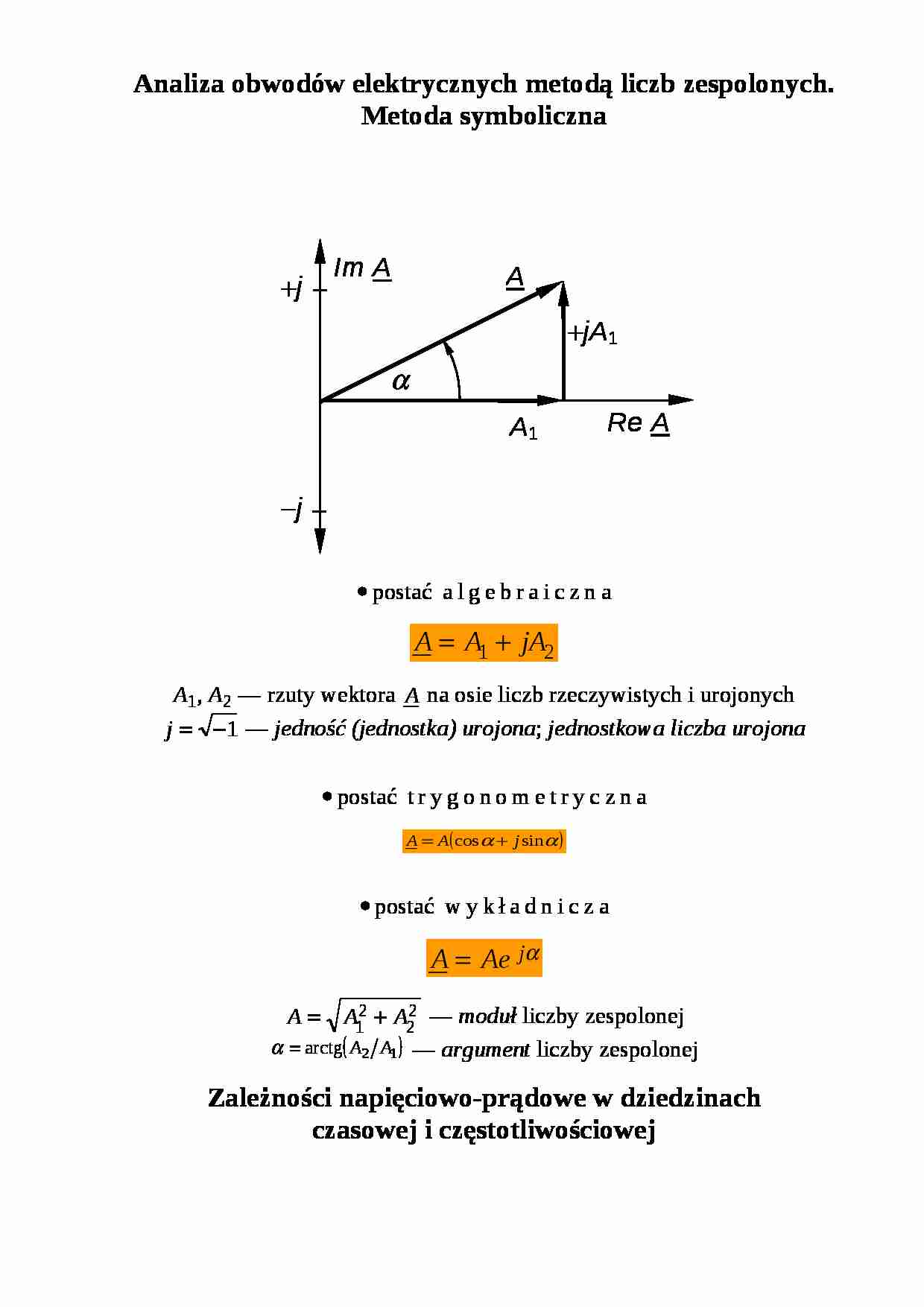


Analiza obwodów elektrycznych metodą liczb zespolonych. Metoda symboliczna postać algebraiczna
A 1, A 2 — rzuty wektora na osie liczb rzeczywistych i urojonych — jedność (jednostka) urojona ; jednostkowa liczba urojona postać trygonometryczna
postać wykładnicza
— moduł liczby zespolonej — argument liczby zespolonej
Zależności napięciowo-prądowe w dziedzinach czasowej i częstotliwościowej gdzie:
— moduł impedancji
— argument impedancji (przesunięcie fazowe)
— rezystancja obwodu
— reaktancja obwodu
gdzie:
— moduł admitancji
— argument admitancji (przesunięcie fazowe)
— konduktancja obwodu
— susceptancja obwodu
Zatem
amplituda wartość skuteczna Prawo Ohma Połączenie szeregowe impedancji
Połączenie równoległe impedancji
Prawo Ohma c.d. — moduł napięcia — argument napięcia (przesunięcie fazowe)
L (1/ C ) X 0, U X 0 u i 0 charakter indukcyjny
L (1/ C ) X 0, U X 0 u i 0 charakter pojemnościowy
L (1/ C ) X 0, U X 0 u i 0 charakter rezystancyjny → rezonans napięć
gdzie:
gdzie:
Moc prądu przemiennego Współczynnik mocy Założenia:
... zobacz całą notatkę






Komentarze użytkowników (0)