To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
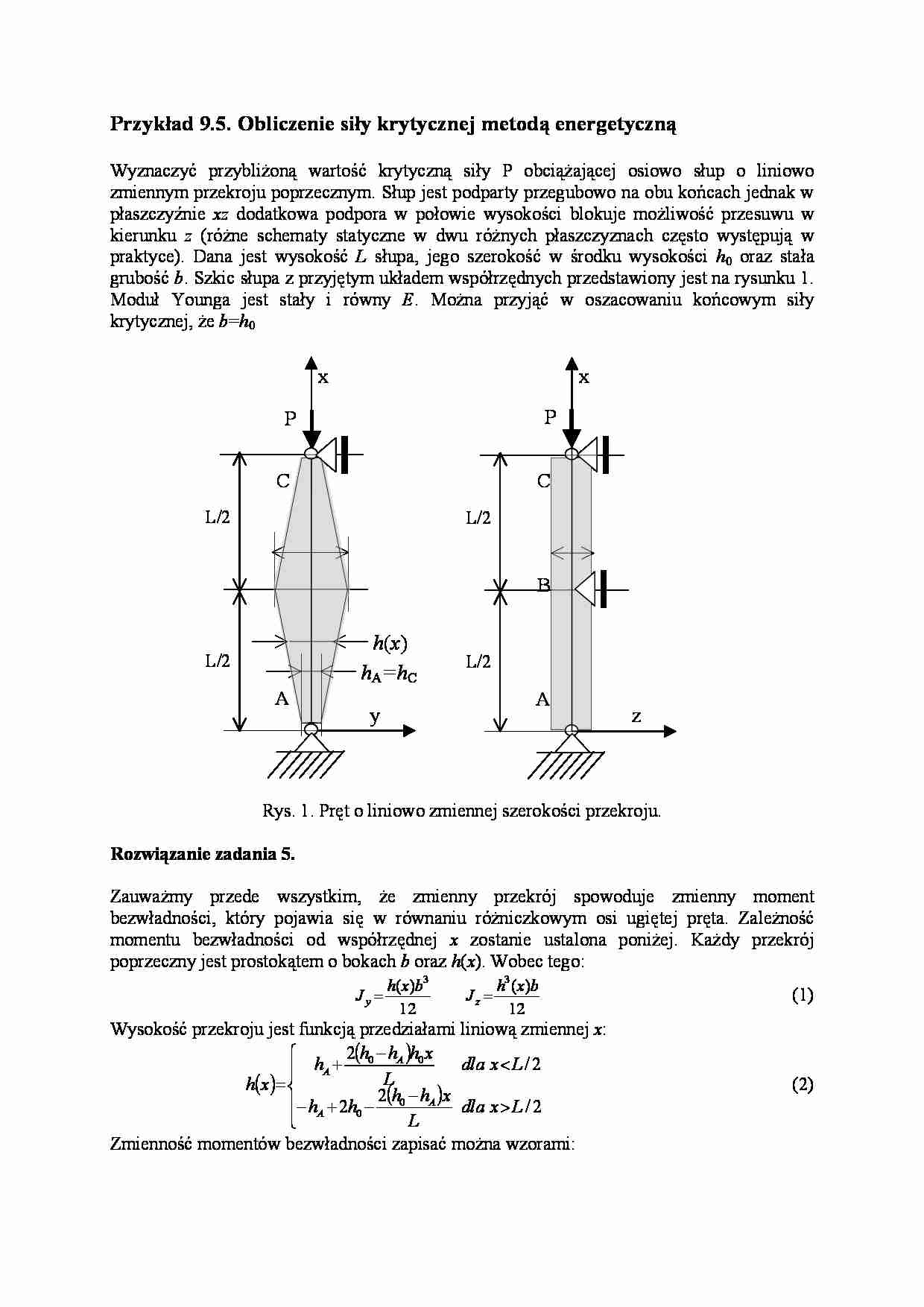


Przykład 9.5. Obliczenie siły krytycznej metodą energetyczną
Wyznaczyć przybliżoną wartość krytyczną siły P obciążającej osiowo słup o liniowo
zmiennym przekroju poprzecznym. Słup jest podparty przegubowo na obu końcach jednak w
płaszczyźnie xz dodatkowa podpora w połowie wysokości blokuje możliwość przesuwu w
kierunku z (różne schematy statyczne w dwu różnych płaszczyznach często występują w
praktyce). Dana jest wysokość L słupa, jego szerokość w środku wysokości h0 oraz stała
grubość b. Szkic słupa z przyjętym układem współrzędnych przedstawiony jest na rysunku 1.
Moduł Younga jest stały i równy E. Można przyjąć w oszacowaniu końcowym siły
krytycznej, że b=h0
x
x
P
P
C
C
L/2
L/2
h0
b
B
B
h(x)
hA=hC
L/2
A
L/2
A
y
z
Rys. 1. Pręt o liniowo zmiennej szerokości przekroju.
Rozwiązanie zadania 5.
Zauważmy przede wszystkim, że zmienny przekrój spowoduje zmienny moment
bezwładności, który pojawia się w równaniu różniczkowym osi ugiętej pręta. Zależność
momentu bezwładności od współrzędnej x zostanie ustalona poniżej. Każdy przekrój
poprzeczny jest prostokątem o bokach b oraz h(x). Wobec tego:
Jy =
h( x)b3
12
Jz =
h3 ( x)b
12
Wysokość przekroju jest funkcją przedziałami liniową zmiennej x:
2(h0 − hA )h0 x
dla x L / 2
L
Zmienność momentów bezwładności zapisać można wzorami:
(1)
(2)
3
b
2(h0 − hA )h0 x
dla x L / 2
0
A
12
L
3
b
2(h0 − hA )h0 x
dla x L / 2
A
0
L
12
Dla pręta o zmiennym przekroju, znalezienie siły krytycznej z warunku istnienia niezerowego
rozwiązania równania różniczkowego osi ugiętej słupa może się okazać skomplikowane.
Równanie różniczkowe osi ugiętej zapisuje się w obu przedziałach zmienności przekroju
następująco (dla przykładu zapisano jedynie równanie dla ugięcia w płaszczyźnie xy):
3
b
2(h0 − hA )h0 x 3
xy
x y′′(x)+ Pkr y(x)= 0 dla x L / 2
0
kr
12 A
L
Rozwiązanie równania (4), (nawet dla liniowo zmiennego przekroju) jest trudne. Aby ominąć
tę trudność zastosujemy metodę energetyczną. Zgodnie z tą metodą najlepszym przybliżeniem
siły krytycznej będzie:
∫ EJ (x)(v′′( x)) dx
Pkr = min 0 L
2
v∈V
∫0 (v′( x)) dx
L
2
(5)
We wzorze (5) v(x) należy do pewnej rodziny funkcji kinematycznie dopuszczalnych V, to
znaczy takich, które spełniają warunki zamocowania i są ciągłe. Aby wzór (5) mógł być
zastosowany funkcja v(x) powinna być dwukrotnie różniczkowalna i obie te pochodne musza
być całkowalne w kwadracie. Minimum osiąga się dla funkcji v(x)=y(x), która jest
rozwiązaniem zagadnienia wyboczenia. Nie zawsze jednak uda się tak zdefiniować rodzinę
funkcji próbnych V, aby rozwiązanie (nieznane!) do niej należało. Należy się
(…)
… w przegubach podporowych są równe zeru, indeksy y i z oznaczają odpowiednio
rzuty wektora momentu na oś y i z).
Kinematyczne warunki wymienione sa poniżej (zerowanie się ugięć na podporach):
y(0)=0, y(L)=0
(8)
z(0)=0, z(L/2)=0, z(L)=0
(9)
Funkcja y(x) taka, że jej druga pochodna przyjmuje wartości zerowe na podporach może być
znaleziona w następujący sposób (ograniczając się do wielomianów w wyborze postaci…
... zobacz całą notatkę






Komentarze użytkowników (0)