To tylko jedna z 10 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


s
˛z
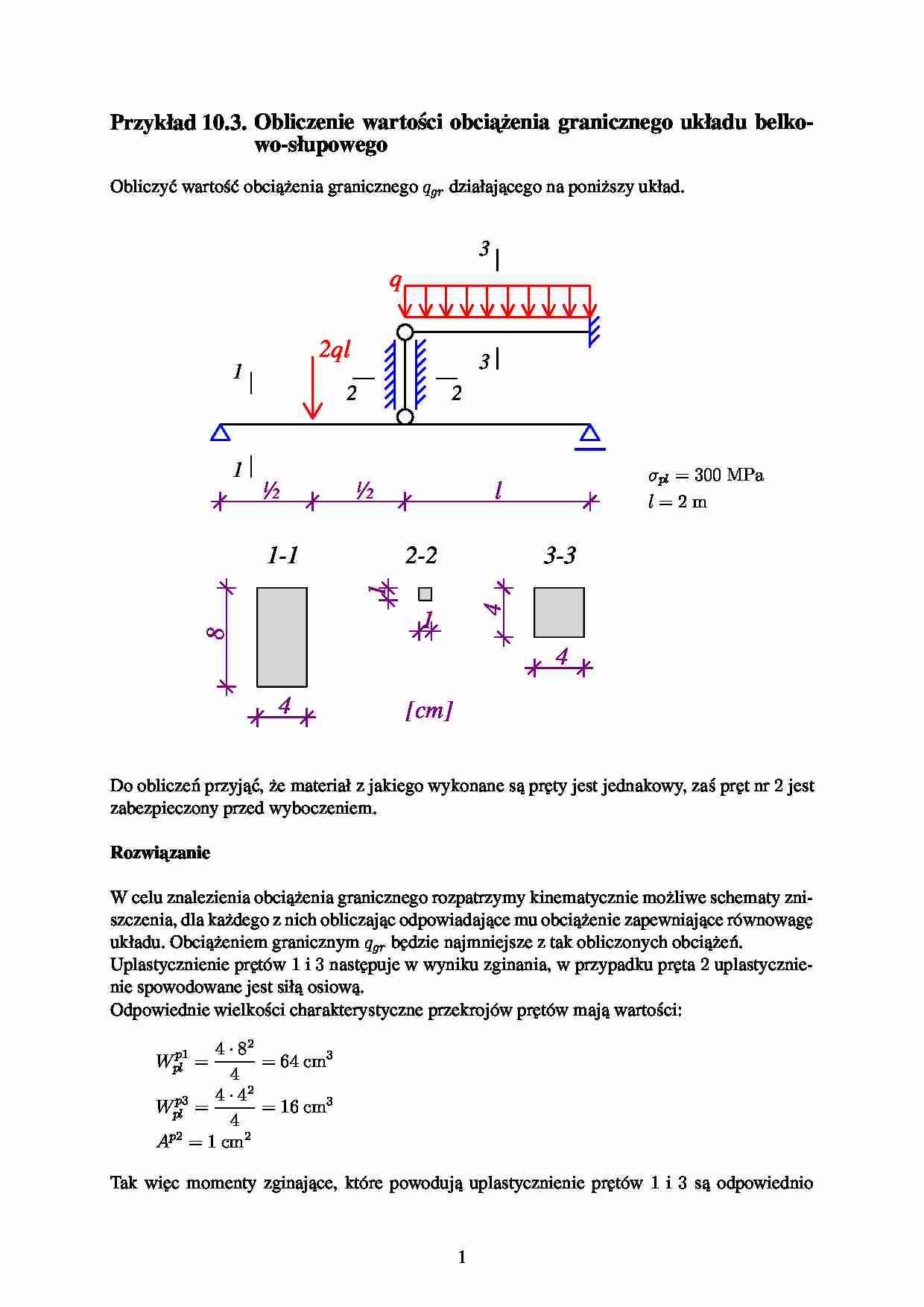
Przykład 10.3. Obliczenie warto´ ci obcia˙ enia granicznego układu belkowo-słupowego
Obliczy´ warto´ c obcia˙ enia granicznego qgr działajacego na poni˙ szy układ.
c
s´
˛z
˛
z
3
q
2ql
3
1
2
2
1
⁄
l2
⁄
2-2
3-3
4
1
1-1
σpl = 300 MPa
l=2m
l
l2
8
1
4
4
[cm]
Do oblicze´ przyja´ , ze materiał z jakiego wykonane sa pr˛ ty jest jednakowy, za´ pr˛ t nr 2 jest
n
˛c ˙
˛ e
s e
zabezpieczony przed wyboczeniem.
Rozwiazanie
˛
W celu znalezienia obcia˙ enia granicznego rozpatrzymy kinematycznie mo˙ liwe schematy zni˛z
z
szczenia, dla ka˙ dego z nich obliczajac odpowiadajace mu obcia˙ enie zapewniajace równowag˛
z
˛
˛
˛z
˛
e
układu. Obcia˙ eniem granicznym qgr b˛ dzie najmniejsze z tak obliczonych obcia˙ en.
˛z
e
˛z ´
Uplastycznienie pr˛ tów 1 i 3 nast˛ puje w wyniku zginania, w przypadku pr˛ ta 2 uplastyczniee
e
e
nie spowodowane jest siła osiowa.
˛
˛
Odpowiednie wielko´ci charakterystyczne przekrojów pr˛ tów maja warto´ci:
s
e
˛
s
4 · 82
= 64 cm3
4
4 · 42
p3
Wpl =
= 16 cm3
4
Ap2 = 1 cm2
p1
Wpl =
Tak wi˛ c momenty zginajace, które powoduja uplastycznienie pr˛ tów 1 i 3 sa odpowiednio
e
˛
˛
e
˛
1
równe:
p1
p1
Mpl = σpl · Wpl = 300 · 103 · 64 · 10−6 = 19,2 kNm
p3
p3
Mpl = σpl · Wpl = 300 · 103 · 16 · 10−6 = 4,8 kNm
Do uplastycznienia pr˛ ta 2 dochodzi, gdy siła normalna w tym pr˛ cie ma warto´ c
e
e
s´
p2
Spl = σpl · Ap2 = 300 · 103 · 1 · 10−4 = 30 kN
Rozpatruje si˛ uplastycznienie tych przekrojów pr˛ tów 1 i 3, w których wyst˛ puja ekstrema
e
e
e ˛
momentów zginajacych, bad´ te˙ w pr˛ cie nr 2, na który działa obcia˙ enie osiowe.
˛
˛z z
e
˛z
Poni˙ szy rysunek przedstawia układ rozło˙ ony na pojedyncze pr˛ ty. Zaznaczono na nim rówz
z
e
nie˙ schematycznie punkty, w których mo˙ na spodziewa´ si˛ powstania przegubów (punkt B
z
z
c e
oznacza punkt nale˙ acy do pr˛ ta 3, odpowiadajacy miejscu wyst˛ powania lokalnego ekstremum
z˛
e
˛
e
momentu zginajacego).
˛
q
B
A
S
S
S
2ql
S
D
⁄
l2
C
⁄
l
l2
Przy konstruowaniu kinematycznie dopuszczalnych schematów zniszczenia nale˙ y pami˛ ta c, ze
z
e ´ ˙
nale˙ y przyjmowa´ kierunek przemieszczenia układu w taki sposób, aby praca sił zewn˛ trznych
z
c
e
na tych przemieszczenia była dodatnia. Jednocze´nie praca sił wewn˛ trznych musi by´ ujemna,
s
e
c
a co za tym idzie, przyj˛ te momenty plastyczne musza mie´ takie zwroty, aby przeciwdziała´
e
˛
c
c
zało˙ onym obrotom.
z
2
Schemat I - uplastycznienie przekrojów A i B
q
δ
B
A
p3
Mpl
p3
Mpl
p3
S Mpl
x
l
Z równania pracy wirtualnej otrzymujemy
q·x·
δ
+ q · (l − x) ·
2
ql
=
=⇒
2
δ
δ
p3 δ
p3
− Mpl · − 2 · Mpl ·
=0
=⇒
2
x
l−x
p3
2
l + x Mpl
1
p3
+
Mpl
=⇒
q=2
x l−x
x (l − x) l
Nieznana warto´ c x mo˙ na łatwo obliczy´ korzystajac z faktu, ze długo´ c odcinka x musi
˛
s´
z
c
˛
˙
s´
dq(x)
˛
odpowiada´ minimalnej warto´ci obcia˙ enia q, tak wi˛ c dx = 0. Stad
c
s
˛z
e
dq (x)
=0
dx
p3
=⇒
=⇒
x (l − x) − (l + x) (l − 2x) Mpl
2
=0
l
x2 (l − x)2
p3
lx − x2 − l2 + 2lx − lx + 2x2 Mpl
2
=0
l
x2 (l − x)2
=⇒
=⇒
p3
=⇒
2
x2 + 2lx − l2 Mpl
(…)
…
<
p2
Spl = 30kN
T
x
19,2
3,43 (+)
(-)
(+)
8,23
(-)
. kN
(-)
4,11
7,54
´
Zerowanie si˛ wykresu siły tnacej w odległo´ci x od podpory A swiadczy o wyst˛ powaniu
e
˛
s
e
w tym miejscu lokalnego ekstremum momentu zginajacego.
˛
VA − qgr · x = 0
=⇒
x=
VA
qgr
p3
Mmax = VA · x − Mpl − qgr · x ·
=⇒
x
2
x=
288
35
204
35
Mmax =
=⇒
Mmax
=⇒
Mmax
x=
72
m ≈ 1,41m
51
=⇒
288 72
204 72 36
·
− 4,8 −
·
·
35 51
35 51 51
6912 24 3456
−
−
=⇒
=
595
5
595
120
=
kNm ≈ 1,01kNm
119
=⇒
=⇒
=⇒
4,8
M
1,01
. kNm
1,41 m
15,09
19,2
Warunki plastyczno´ci sa spełnione (|M | 19,2kNm w przypadku pr˛ ta nr 1 i |M | 4,8kNm
s
˛
e
w przypadku pr˛ ta nr 3 oraz |S|
e
Spl w przypadku pr˛ ta nr 2). Oznacza to, ze otrzymane
e
˙
rozwiazanie jest rozwiazaniem zupełnym, poniewa˙ spełnia wszystkie równania: warunki kine˛
˛
z
matyczne, równania…
... zobacz całą notatkę






Komentarze użytkowników (0)