To tylko jedna z 10 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
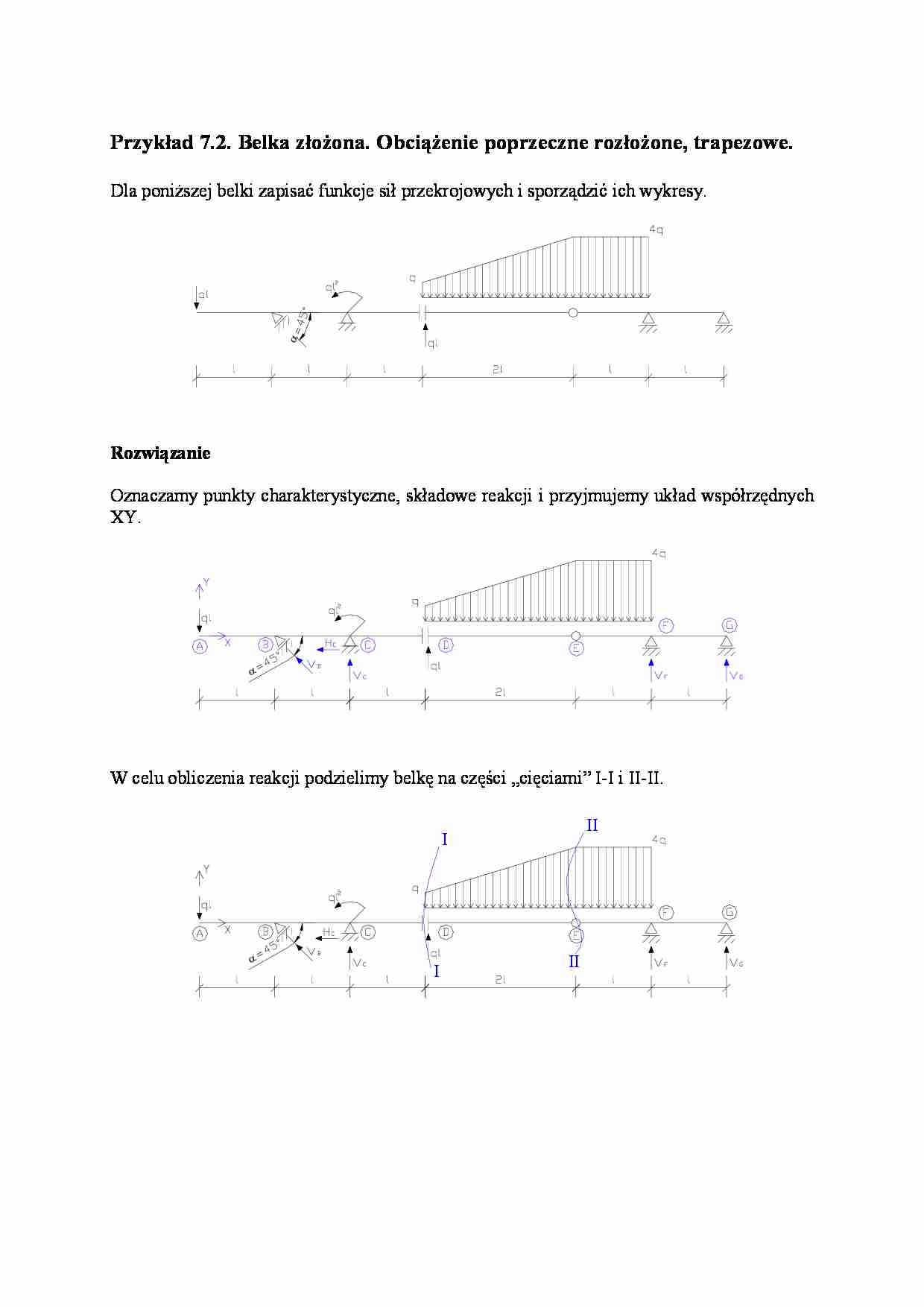


Przykład 7.2. Belka złożona. Obciążenie poprzeczne rozłożone, trapezowe. Dla poniższej belki zapisać funkcje sił przekrojowych i sporządzić ich wykresy. α = Rozwiązanie Oznaczamy punkty charakterystyczne, składowe reakcji i przyjmujemy układ współrzędnych XY. α = W celu obliczenia reakcji podzielimy belkę na części „cięciami” I-I i II-II. Ι ΙΙ α = Ι ΙΙ W miejscach „cięć” uzewnętrzniamy niezerowe siły działające w połączeniach. α = Wykorzystując równania równowagi dla poszczególnych fragmentów obliczymy reakcje. Dla fragmentu II: Rozpatrywany fragment belki obciążony jest m. in. obciążeniem poprzecznym trapezowym. W celu uwzględnienia tego obciążenia należy podzielić je na obciążenie prostokątne i trójkątne i dokonać ich superpozycji. ( ) ( ) 2 2 0 2 3 1 2 4 2 1 2 2 1 2 2 0 4 0 2 4 2 1 0 ql M l l q q l l q M l ql M ql T l q q T ql P D D E E E y = ⇒ = ⋅ ⋅ ⋅ − ⋅ − ⋅ ⋅ ⋅ − + ⋅ ⇔ = − = ⇒ = ⋅ + ⋅ − − ⇔ = ∑ ∑ Dla fragmentu III: ql V ql ql V ql l q T V V P ql V ql ql V l l l q l T l V M N P G G E G F y F F E F G E x 6 0 4 4 14 0 4 0 14 0 6 2 4 0 2 1 4 2 0 0 0 − = ⇒ = − − + ⇒ = ⋅ − + + ⇔ = = ⇒ = − ⋅ − ⇒ = ⋅ + ⋅ ⋅ − ⋅ + ⋅ ⇔ = = ⇔ = ∑ ∑ ∑ Dla fragmentu II: 0 0 = ⇒ = ⇔ = ∑ D E D x N N N P 2 Dla fragmentu I: ql V ql ql V ql V sin V P ql H H ql N H cos V P ql V V 5ql ql ql sin l V ql M ql l sin V l ql M C C C B y C C D C B x B B o B D B C 4 0 2 1 2 5 0 0 5 0 2 1 2 5 0 0 2 5 0 2 1 0 2 45 2 0 2 0 2 2 2 2 − = ⇒ = ⋅ − = ⇒ = − + ⋅ ⇔ = = ⇒ = + ⋅ − ⇒ = + + ⋅ − ⇔ = = ⇒ = ⋅ + − ⇒ ⇒ = − − ⋅ ⋅ + − ⇒ = − − ⋅ ⋅ + ⋅ − ⇔ = ∑ ∑ ∑ α α α Tak więc na belkę działają następujące obciążenia: α = √2 W celu znalezienia funkcji sił przekrojowych, podobnie jak w Przykładzie 7.1. dokonywać będziemy „przecięć” belki przekrojami pomiędzy punktami charakterystycznymi.
(…)
…:
TDp = T (0 ) = ql
3q
2
⋅ (2l ) − q ⋅ (2l ) + ql = −4 ql
4l
p
M D = M (0 ) = 2ql 2
TEl = T (2l ) = −
1 (2l ) 1
2
l
M E = M (2l ) = − q
− q (2l ) + ql (2l ) + 2ql 2 = 0
4
l
2
Jak widać funkcja T ( x ) zmienia znak, co oznacza, że punkcie zmiany znaku występuje
ekstremum lokalne M (x ) . W celu znalezienia punktu zerowania się funkcji T ( x ) należy
rozwiązać równanie kwadratowe:
3q 2
−
x2 − qx2 + ql…
… ) − q ⋅ (2l ) + ql = −4 ql
2
4l
M D = M (0 ) = 2ql 2
p
1 (2l ) 1
3
M E = M (2l ) = − q − q (2l ) + ql (2l ) + 2ql 2 = 0
l 2
4 l 2
Jak widać funkcja T ( x ) zmienia znak, co oznacza, że punkcie zmiany znaku występuje
ekstremum lokalne M (x ) . W celu znalezienia punktu zerowania się funkcji T ( x ) należy
rozwiązać równanie kwadratowe:
3q 2
− x2 − qx2 + ql = 0 , x2 ∈ 0 ,2l
4l
∆= (− q )2 − 4 ⋅ − 3q…
… wykresu T ( x )
4. Jeżeli na danym odcinku nie działa siła poprzeczna rozłożona, to wykres T ( x ) na tym
odcinku jest stały (T = const. ).
5. Na odcinku, na którym działa obciążenie poprzeczne rozłożone, liniowo zmienne,
wykres siły T ( x ) jest parabolą.
6. W miejscu występowania teleskopu siła T jest równa 0, o ile nie występuje tam siła
skupiona.
III. Dotyczy wykresu M (x )
4. Na odcinku…
... zobacz całą notatkę






Komentarze użytkowników (0)