To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę

Przykład 7.5. Naprężenia styczne pręta skręcanego
Znaleźć naprężenia styczne w obu częściach pręta cienkościennego skręcanego.
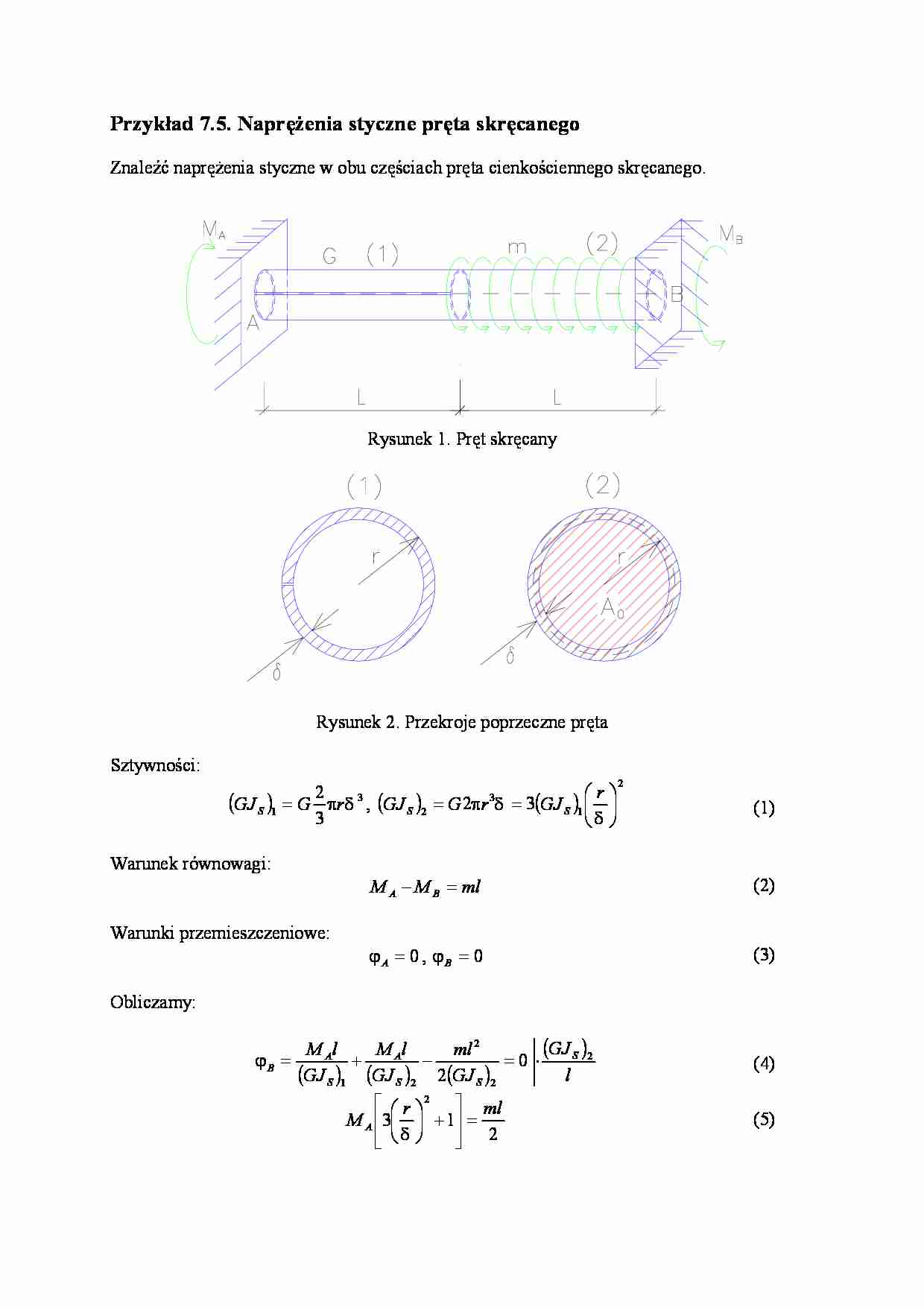
Rysunek 1. Pręt skręcany
Rysunek 2. Przekroje poprzeczne pręta
Sztywności:
(GJ S )1
2
r
= G πrδ 3 , (GJ S )2 = G 2πr 3δ = 3(GJ S )1
3
δ
2
(1)
Warunek równowagi:
M A − M B = ml
(2)
ϕ A = 0 , ϕB = 0
(3)
Warunki przemieszczeniowe:
Obliczamy:
ϕB =
(GJ S )2
M Al
M Al
ml 2
+
−
=0 ⋅
(GJ S )1 (GJ S )2 2(GJ S )2
l
r 2 ml
M A 3 + 1 =
δ
2
(4)
(5)
1
ml
,
2 r 2
3 + 1
δ
2
r
1 + 6
ml
δ .
MB = −
2
2
r
1 + 3
δ
MA =
(6)
Jeśli r / δ = 10 to:
ml
,
602
601ml
MB = −
.
602
MA =
(7)
Naprężenia
ml
1
3 ml
=
,
1 2
602 δ 2πr 1204π δ 2 r
3
601ml 1
601 ml
τ2 = −
=−
2
602 2πr δ
1204π r 2δ
τ1 =
(8)
τ 2 601 δ 601 1 60.1
=
=
=
≈ 20
3 r
3 10
3
τ1
(9)
Stosunek naprężeń:
Sztywności części drugiej jest 300 razy większa, lecz naprężenia w tej części są 20 razy
większe od naprężeń w części pierwszej.
Jeżeli porównać wskaźniki wytrzymałości obu części, to otrzymujemy:
(WS )2 2πr 2δ
r
=
= 3 = 30 .
1 2
(WS )1
δ
δ 2πr
3
2
(10)
... zobacz całą notatkę




Komentarze użytkowników (0)