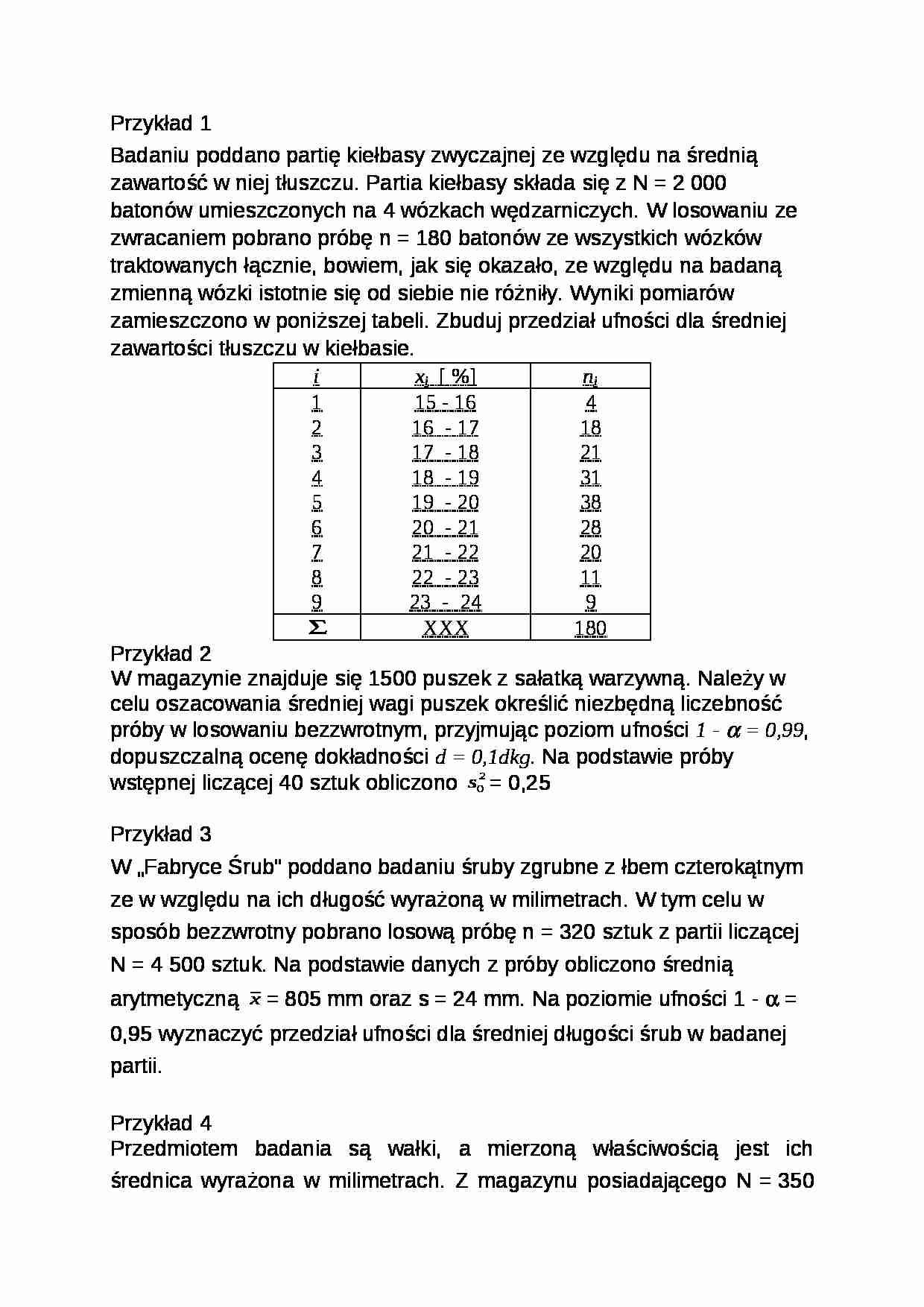
Przykład 1
Badaniu poddano partię kiełbasy zwyczajnej ze względu na średnią zawartość w niej tłuszczu. Partia kiełbasy składa się z N = 2 000 batonów umieszczonych na 4 wózkach wędzarniczych. W losowaniu ze zwracaniem pobrano próbę n = 180 batonów ze wszystkich wózków traktowanych łącznie, bowiem, jak się okazało, ze względu na badaną zmienną wózki istotnie się od siebie nie różniły. Wyniki pomiarów zamieszczono w poniższej tabeli. Zbuduj przedział ufności dla średniej zawartości tłuszczu w kiełbasie.
i x i [ %]
n i 1
2
3
4
5
6
7
8
9
15 - 16
16 - 17
17 - 18
18 - 19
19 - 20
20 - 21
21 - 22
22 - 23
23 - 24
4
18
21
31
38
28
20
11
9
XXX
180
Przykład 2 W magazynie znajduje się 1500 puszek z sałatką warzywną. Należy w celu oszacowania średniej wagi puszek określić niezbędną liczebność próby w losowaniu bezzwrotnym, przyjmując poziom ufności 1 - = 0,99 , dopuszczalną ocenę dokładności d = 0,1dkg . Na podstawie próby wstępnej liczącej 40 sztuk obliczono = 0,25
Przykład 3 W „Fabryce Śrub” poddano badaniu śruby zgrubne z łbem czterokątnym ze w względu na ich długość wyrażoną w milimetrach. W tym celu w sposób bezzwrotny pobrano losową próbę n = 320 sztuk z partii liczącej N = 4 500 sztuk. Na podstawie danych z próby obliczono średnią arytmetyczną = 805 mm oraz s = 24 mm. Na poziomie ufności 1 - = 0,95 wyznaczyć przedział ufności dla średniej długości śrub w badanej partii. Przykład 4
Przedmiotem badania są wałki, a mierzoną właściwością jest ich średnica wyrażona w milimetrach. Z magazynu posiadającego N = 350 sztuk wałków pobrano zwrotną próbę losową o liczebności n = 20 i zmierzono ich średnicę. Otrzymane wyniki zawarto w tabeli. Znajdź wartości liczbowe końców przedziału ufności przy przyjętym poziomie ufności 1 - = 0,99. i 1
2
3
4
5
6
7
8
9
10
x i [ mm] 49,0
48,5
47,3
49,7
51,2
50,2
50,8
48,8
50,4
50,1
i 11
12
13
14
15
16
17
18
19
20
x i [ mm] 48,7
49,2
51,0
50,7
50,3
48,8
(…)
… skupu płodów rolnych w danym dniu 180 worków ze zbożem pochodzącym od pięciu z nich i otrzymano dane:
Tabela 4.8 Tabela robocza
Rolnik h
Liczba
worków Nh
Wilgotność
w %
1
2
3
4
5
300
520
540
280
360
15,0
19,2
22,3
14,1
9,2
4,34
9,25
10,20
4,10
5,27
2 000
-
-
l=5
N
-
-
Źródło: dane umowne. Na poziomie istotności = 0,05 oszacować dla danego obszaru skupu przeciętne nawilgocenie zboża. Dla przyjętej…
…. Otrzymane wyniki zawarto w tabeli:
Tabela. Dane do przykładu 7
i
1
2
3
4
5
6
7
8
9
10
xi
7,2
7,6
7,8
7,1
7,3
7,5
7,7
7,8
7,4
7,5
11
12
13
14
15
7,3
7,5
7,7
7,8
7,1
112,30
Na poziomie ufności 1 - = 0,96 zbuduj przedział ufności dla odchylenia standardowego w zakresie natężenia białego światła w partii badanych lamp.
Przykład 8 W celu zbadania odsetka rowerzystów, którzy spowodowali wypadki drogowe będąc…
... zobacz całą notatkę





Komentarze użytkowników (0)