jpeg.
Notatka to materiały z ćwiczeń zawierające rozwiązania zadań wraz z zestawami – treścią zadań.
Notatka pozwoli na usystematyzowanie i uzupełnienie wiedzy z przedmiotu metoda reprezentacyjna. Pozwoli na przygotowanie się do zajęć i egzaminu.
Przykład 1
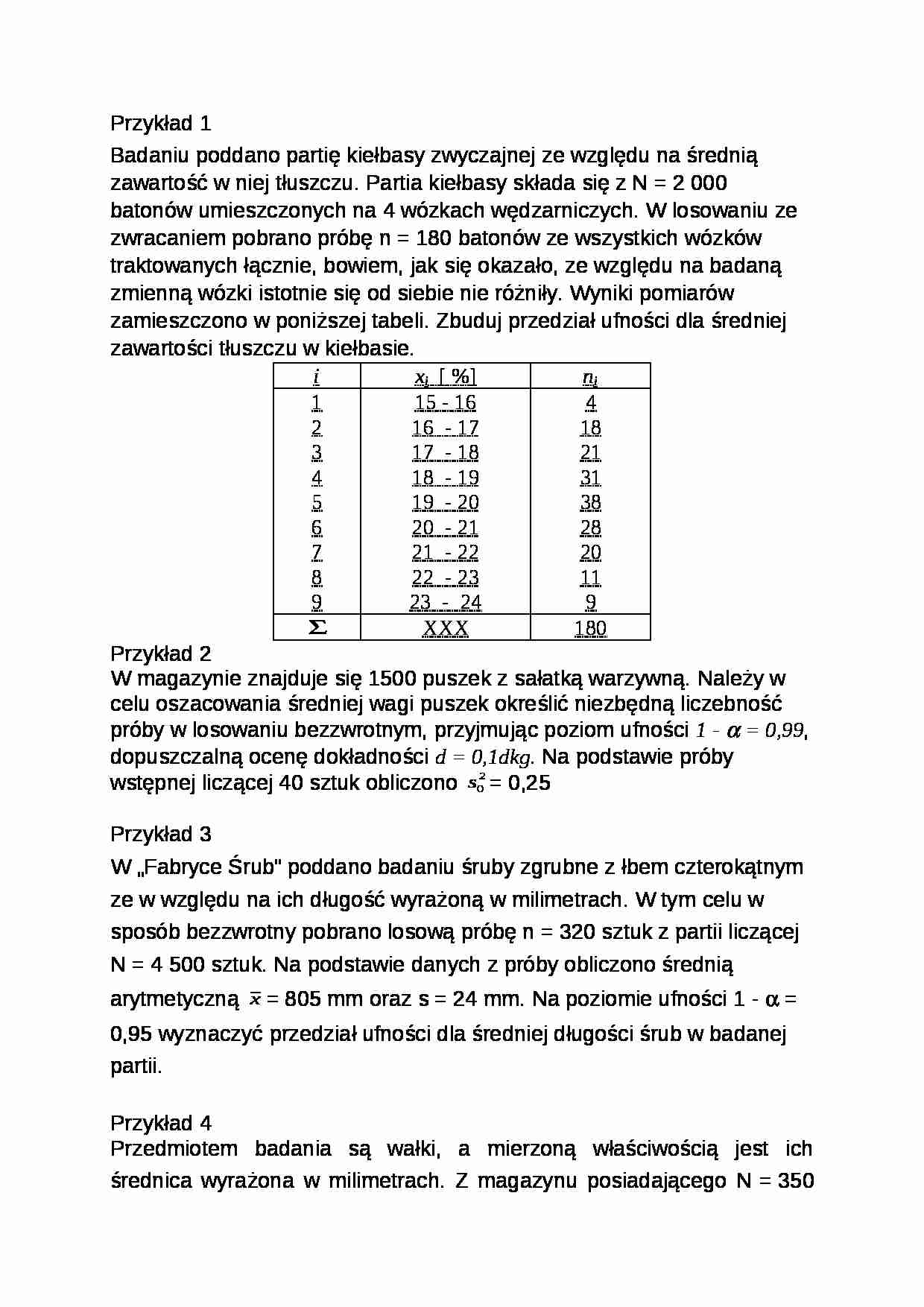
Badaniu poddano partię kiełbasy zwyczajnej ze względu na średnią zawartość w niej tłuszczu. Partia kiełbasy składa się z N = 2 000 batonów umieszczonych na 4 wózkach wędzarniczych. W losowaniu ze zwracaniem pobrano próbę n = 180 batonów ze wszystkich wózków traktowanych łącznie, bowiem, jak się okazało, ze względu na badaną zmienną wózki istotnie się od siebie nie różniły. Wyniki pomiarów zamieszczono w poniższej tabeli. Zbuduj przedział ufności dla średniej zawartości tłuszczu w kiełbasie.
i
xi [ %]
ni
1
2
3
4
5
6
7
8
9
15 - 16
16 - 17
17 - 18
18 - 19
19 - 20
20 - 21
21 - 22
22 - 23
23 - 24
4
18
21
31
38
28
20
11
9
XXX
180
Przykład 2 W magazynie znajduje się 1500 puszek z sałatką warzywną. Należy w celu oszacowania średniej wagi puszek określić niezbędną liczebność próby w losowaniu bezzwrotnym, przyjmując poziom ufności 1 - = 0,99, dopuszczalną ocenę dokładności d = 0,1dkg. Na podstawie próby wstępnej liczącej 40 sztuk obliczono = 0,25
Przykład 3 W „Fabryce Śrub” poddano badaniu śruby zgrubne z łbem czterokątnym ze w względu na ich długość wyrażoną w milimetrach. W tym celu w sposób bezzwrotny pobrano losową próbę n = 320 sztuk z partii liczącej N = 4 500 sztuk. Na podstawie danych z próby obliczono średnią arytmetyczną = 805 mm oraz s = 24 mm. Na poziomie ufności 1 - = 0,95 wyznaczyć przedział ufności dla średniej długości śrub w badanej partii. Przykład 4
Przedmiotem badania są wałki, a mierzoną właściwością jest ich średnica wyrażona w milimetrach. Z magazynu posiadającego N = 350 sztuk wałków pobrano zwrotną próbę losową o liczebności n = 20 i zmierzono ich średnicę. Otrzymane wyniki zawarto w tabeli. Znajdź wartości liczbowe końców przedziału ufności przy przyjętym poziomie ufności 1 - = 0,99. i
1
2
3
4
5
6
7
8
9
10
xi [ mm]
49,0
48,5
47,3
49,7
51,2
50,2
50,8
48,8
50,4
50,1
i
11
12
13
14
15
16
17
18
19
20
xi [ mm]
48,7
49,2
51,0
50,7
50,3
48,8
49,2
50,1
50,3
49,9
Przykład 4 cd Oszacować metodą przedziałową wariancję średnicy.
Przykład 5
Z partii N = 14 000 sztuk dyskietek wybrano w sposób bezzwrotny próbę o liczebności n = 1 500 sztuk i zbadano je ze względu na szum wirowania. Stwierdzono, iż zbyt wielkim szumem charakteryzuje się m = 124 dyskietki. Na poziomie ufności 1 - =0,99 wyznaczyć końce przedziału ufności dla frakcji dyskietek wadliwych.
(…)
… skupu płodów rolnych w danym dniu 180 worków ze zbożem pochodzącym od pięciu z nich i otrzymano dane:
Tabela 4.8 Tabela robocza
Rolnik h
Liczba
worków Nh
Wilgotność
w %
Liczebność
próby
nh 1
2
3
4
5
300
520
540
280
360
15,0
19,2
22,3
14,1
9,2
4,34
9,25
10,20
4,10
5,27
0,15
0,26
0,27
0,14
0,18
27
47
49
25
32
2,250
4,992
6,021
1,974
1,656
0,0241
0,0514
0,0567
0,0228
0,0293
0.0036
0,0134
0,0153
0,0032…
…. Otrzymane wyniki zawarto w tabeli:
Tabela. Dane do przykładu 7
i
1
2
3
4
5
6
7
8
9
10
xi
7,2
7,6
7,8
7,1
7,3
7,5
7,7
7,8
7,4
7,5
11
12
13
14
15
7,3
7,5
7,7
7,8
7,1
112,30
Na poziomie ufności 1 - = 0,96 zbuduj przedział ufności dla odchylenia standardowego w zakresie natężenia białego światła w partii badanych lamp.
Przykład 8 W celu zbadania odsetka rowerzystów, którzy spowodowali wypadki drogowe będąc…
... zobacz całą notatkę





Komentarze użytkowników (0)