To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
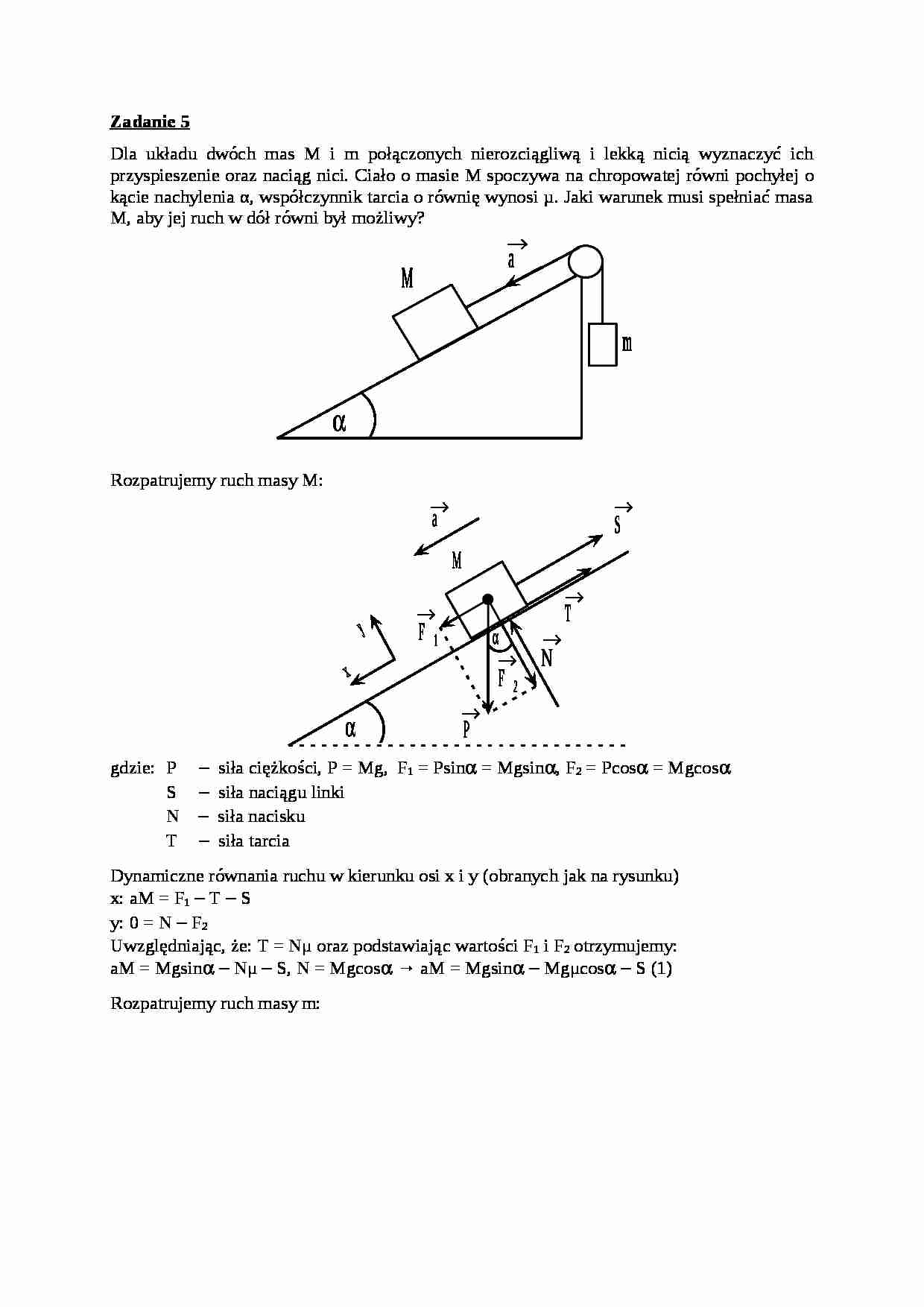

Zadanie 5
Dla układu dwóch mas M i m połączonych nierozciągliwą i lekką nicią wyznaczyć ich przyspieszenie oraz naciąg nici. Ciało o masie M spoczywa na chropowatej równi pochyłej o kącie nachylenia α, współczynnik tarcia o równię wynosi µ. Jaki warunek musi spełniać masa M, aby jej ruch w dół równi był możliwy?
Rozpatrujemy ruch masy M:
gdzie: P − siła ciężkości, P = Mg, F1 = Psinα = Mgsinα, F2 = Pcosα = Mgcosα
S − siła naciągu linki
N − siła nacisku
T − siła tarcia
Dynamiczne równania ruchu w kierunku osi x i y (obranych jak na rysunku)
x: aM = F1 − T − S
y: 0 = N − F2 Uwzględniając, że: T = Nμ oraz podstawiając wartości F1 i F2 otrzymujemy:
aM = Mgsinα − Nμ − S, N = Mgcosα → aM = Mgsinα − Mgμcosα − S (1)
Rozpatrujemy ruch masy m:
gdzie: Q − siła ciężkości, P = mg, S − j.w.
Dynamiczne równanie ruchu:
am = S − Q → am = S − mg (2)
dodając stronami równania (1) i (2) otrzymamy wzór na przyspieszenie układu:
aM + am = Mgsinα − Mgμcosα − mg → aby ruch masy M w dół równi był możliwy musi być: a 0, czyli: Mg(sinα − μcosα) − mg 0
stąd otrzymujemy: .
... zobacz całą notatkę




Komentarze użytkowników (0)